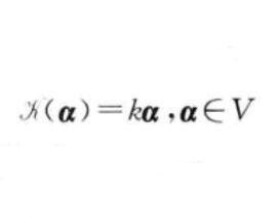數乘變換
數乘變換
數乘變換(transformation of scalar multiplicalion)是一種線性變換，設V是數域P上的一個線性空間，k是P中的一個數，對任意α∈V，由σ(α)=kα所決定的線性變換σ，稱為數乘變換，記為k*，這樣1*就是單位變換，0*就是零變換。
設V為數域F上的線性空間，是V到V的一個映射（變換），且滿足條件：
（1）對任意的 有：
（2）對任意的 及任意的實數，有：
則稱為V的 線性變換。
設V是數域F上的線性空間。定義變換為
稱為 恆等變換或單位變換；定義變換為
稱為 零變換，它們都是線性變換。
設V是數域F上的線性空間，，定義變換 為
稱為 數乘變換，數乘變換是線性變換，故線性變換的性質也是數乘變換的性質，參見線性變換。顯然當數乘變換即為恆等變換，數乘變換即為零變換。
(1)設是V的一個線性變換，則：
因為，
(2)線性變換保持向量的線性組合和線性關係式不變，即
若 β是的線性組合：
則有
仍然是的線性組合，且表出係數相同。
同樣若對於有：
則有：
(3)線性變換把線性相關的向量組變為線性相關的向量組。
注 線性變換可能把線性無關的向量組變為線性相關的向量組，譬如零變換。
基本信息
- 所屬問題
- 線性代數（向量空間）
- 所屬學科
- 數學