工具變數法
工具變數法
在模型估計過程中被作為工具使用,以替代模型中與誤差項相關的隨機解釋變數的變數,稱為工具變數。
作為工具變數,必須滿足下述四個條件:
(1)與所替的隨機解釋變數高度相關;
(2)與隨機誤差項不相關;
(3)與模型中其他解釋變數不相關;
(4)同一模型中需要引入多個工具變數時,這些工具變數之間不相關。
選擇一個變數,作為模型中某隨機解釋變數的工具變數,與模型中的其他變數一起構造出相應參數的一個一致估計量,這種估計方法稱為工具變數法。
工具變數法的關鍵是選擇一個有效的工具變數,由於工具變數選擇中的困難,工具變數法本身存在兩方面不足:
一是由於工具變數不是惟一的,因而工具變數估計量有一定的任意性;
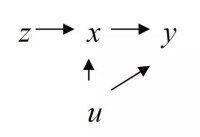
工具變數法
內生解釋變數會造成嚴重的後果:不一致性inconsistent和有偏biased,因為不滿足誤差以解釋變數為條件的期望值為0。產生解釋變數內生一般有三個原因:
一、遺漏變數
二、測量誤差
三、聯立性
第三種情況是無法解決的,前兩種可以採用工具變數(IV)法。IV帶來的唯一壞處是估計方差的增大,也就是說同時採用OLS和IV估計,則前者的方差小於後者。但IV的應用是有前提條件的:1.IV與內生解釋變數相關,2.IV與u不相關。在小樣本情況下,一般用內生解釋變數對IV進行回歸,如果R-sq值很小的話,一般t值也很小,所以對IV質量的評價沒有大的問題,但是當採用大樣本時,情況則相反,往往是t值很大,而R-sq很小,這時如果採用t值進行評價則可能出現問題。這時IV與內生解釋變數之間的相關程度不是太大,但是如果與u之間有輕微的相關的話,則:1、導致很大的不一致性;2、有偏性,並且這種有偏性隨著R-sq趨於0而趨於OLS的有偏性。
所以現在在採用IV時最好採用R-sq或F-sta作為評價標準,另外為了觀測IV與u的關係,可以將IV作為解釋變數放入方程進行回歸,如果其他的係數沒有大的變化,則說明IV滿足第二個條件。