第二類間斷點
數學領域的概念之一
第二類間斷點是指函數的左右極限至少有一個不存在。第二類間斷點有非常多種,如無窮間斷點,振蕩間斷點,單側間斷點,狄利克雷函數間斷點等等,但目前大學數學及考研只要求掌握無窮間斷點與振蕩間斷點,所以詞條只詳解這兩類。
第二類間斷點:函數的左右極限至少有一個不存在。
a.若函數在處的左右極限至少有一個無窮不存在,則稱為f(x)的無窮間斷點。例
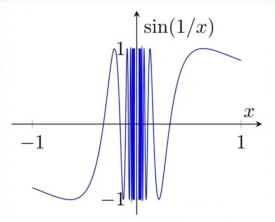
b若函數在處的左右極限至少有一個振蕩不存在,則稱為f(x)的振蕩間斷點。例
設Xo是函數f(x)的間斷點,那麼
如果f(x-)與f(x+)都存在,則稱Xo為f(x)的第一類間斷點。又如果
(i),,或f(x)無意義,則稱Xo為f(x)的可去間斷點。
(ii),,則稱Xo為f(x)的跳躍間斷點。
間斷點分為可去間斷點、跳躍間斷點、無窮間斷點、震蕩間斷點,其中可去間斷點和跳躍間斷點屬於第一類間斷點。在第一類間斷點中,有兩種情況,左右極限存在是前提。左右極限相等,但不等於該點函數值f(x0)或者該點無定義時,稱為可去間斷點,如函數在點處;左右極限在該點不相等時,稱為跳躍間斷點,如函數在處。另外,非第一類間斷點即為第二類間斷點(discontinuity point of the second kind)。