間斷點
間斷點
間斷點是指:在非連續函數y=f(x)中某點處xo處有中斷現象,那麼,xo就稱為函數的不連續點。
間斷點可以分為無窮間斷點和非無窮間斷點,在非無窮間斷點中,還分可去間斷點和跳躍間斷點。如果極限存在就是可去間斷點,不存在就是跳躍間斷點。
設一元實函數f(x)在點x0的某去心鄰域內有定義。如果函數f(x)有下列情形之一:
(1)函數f(x)在點x0的左右極限都存在但不相等、即;
(2)函數f(x)在點x0的左右極限中至少有一個不存在;
(3)函數f(x)在點x0的左右極限都存在且相等,但不等於f(x0)或者f(x)在點x0無定義。
則函數f(x)在點x0為不連續,而點x0稱為函數f(x)的間斷點。
幾種常見類型。
可去間斷點:函數在該點左極限、右極限存在且相等,但不等於該點函數值或函數在該點無定義。如函數在點處。(圖一)
跳躍間斷點:函數在該點左極限、右極限存在,但不相等。如函數在點處。(圖二)
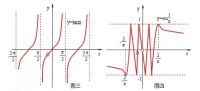
無窮間斷點:函數在該點可以無定義,且左極限、右極限至少有一個不存在,且函數在該點極限為∞。如函數在點處。(圖三)
可去間斷點和跳躍間斷點稱為第一類間斷點,也叫有限型間斷點。其它間斷點稱為第二類間斷點。
由上述對各種間斷點的描述可知,函數f(x)在第一類間斷點的左右極限都存在,而函數f(x)在第二類間斷點的左右極限至少有一個不存在,這也是第一類間斷點和第二類間斷點的本質上的區別。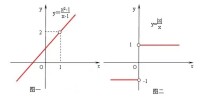

間斷點

間斷點
可去不連續點
1. 考慮以下函數:
點是可去不連續點。
2. 考慮以下函數:
點是跳躍不連續點。
3. 考慮以下函數:
點是第二類不連續點,又稱本性不連續點。