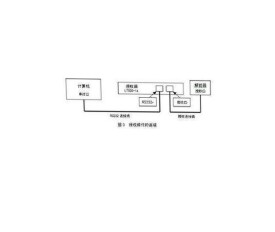
解擾

系統中加入擾碼的目的有三個：

第一，短周期的數字信號具有頻率足夠高的單音，而數字信號的電平也常是相當高的。這種單音可以和載波或調製信號交調，產生非線性產物，落入相鄰通道內，成為對在相鄰通道內傳輸的信號的干擾。但經過擾碼器后，短周期信號被變換為周期足夠長的序列，成為頻率較低的若干電平低的多的單音信號，使它本身和由上述交調產生的單音或者落在載波通道之外，或者電平很低、干擾很小。

第二，在從信息序列中提取定時的系統中，位定時常從通道信號的電平過渡點提取，當過渡點的密度很小時（甚至長時間內沒有）提取定時信號將非常困難；而在輸入序列為周期序列時，很可能發生過渡點過少的情況。擾碼器將保證它本身所輸出的周期性序列有足夠多的過渡點，當擾碼器設計得恰當是，可以得到占碼元速率近半數的過渡點。

第三，當傳輸系統中具有時域均衡器時，擾碼器能與保證定時提取電路的正常工作相似地保證這種均衡器的正常工作。總之，擾碼器起的作用是：如果輸入數字序列是短周期的，將把它按照某種規律變換（擾碼）為長周期，並且使輸出序列（以後將稱為通道序列）中的過判決點（在二進位中即過零點）接近碼總數的一半。解擾器在接收端將被擾碼后的序列還原為輸入發送機的數字序列（消息）。

目前，在多電平傳輸系統中，擾碼和解擾幾乎全在二進位尚未變換為多進位和已反變換為二進位的情況下進行，所以這裡只討論二進位數字的擾碼和解擾問題，但是，討論的過程和結論大都可以推廣到多進位。

最簡單的擾碼方法是在輸入數字序列上加一個最長線性移位寄存器序列，使前者變換為通道序列；相應地在接收端從通道序列中減去同步的同一最長移位寄存器序列，可還原為原數字序列。這個方法在電路上不難實現。這種方法的另一優點是：當通道序列在傳輸中出現碼元差錯時，不會因為加有解擾器而使差錯傳播。這個方法存在的問題在於同步。在有自動均衡的系統中，同步可以在訓練序列的末尾完成；但是一旦失步，必須重新傳輸訓練序列，而且，除非通道序列中有剩餘度，傳輸系統本身不會認識到這種失步。

由於這一原因，即使在有自動均衡的系統中，也多不使用這種相加擾碼器。現在經常使用的擾碼和解擾電路都具有自同步性質。所謂自同步，就是在任何起始狀態下，解擾器能在開始正確地接收已受擾碼序列的一定時間以後，得到同步，輸出正確的還原數據。當接收到的碼元有差錯時，可以在很短時間內恢復同步。儘管如此，由於這些擾碼器和解擾器與最長線性移位寄存器序列有密切的關係，擾碼和解擾過程與產生最長線性移位寄存器序列的方法很相似。