數量性狀遺傳

數量性狀包括兩大類：一是表型連續變異性狀，如牛的泌乳量，農作物的產量，羊毛長度等；二是表型呈非連續變異，而遺傳物質的數量呈潛在的連續變異的性狀，即只有超過某一遺傳閾值時才出現的性狀，如動植物包括人類的抗病力、死亡率以及單胎動物的產仔數等性狀，稱為閾性狀（threshold character或threshold trait）

生物群體內表現連續變異的性狀的遺傳。數量性狀不同於質量性狀。後者如豌豆花色的紅和白及其子粒的圓和皺，玉米子粒的黃和白及其胚乳性質的糯和非糯等；在它們的分離群體內，不同表型間存在非常明顯的差別，即變異是不連續的。數量性狀如個體的高矮、輕重、果實的大小、纖維的長短等，則需要用度量數值表示其表型。在數量性狀的分離群體內，很難根據個體表型的不同在它們之間劃出明確的差別界限，即變異是連續的。數量性狀的發育最易受環境的影響。畜、禽、作物的經濟性狀，絕大多數屬於數量性狀。

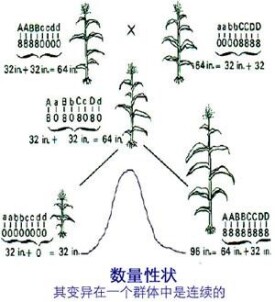
數量性狀遺傳的特點因基因效應不同而異，一般可概括為 3種情況：①某數量性狀表現不同的兩個親本雜交，子一代(F1)的該性狀一般介於兩親之間，其平均數與兩親的中值近似。②子二代(F2)群體的連續差異幅度顯著擴大，一般近似正態分佈，但其平均數仍近似F1。③控制數量性狀發育的基因易受環境影響，即使純合的親本或基因型相同的F1個體間，其表型也會呈現一定幅度的連續變異。所以F2群體變異幅度的顯著擴大，除由於F2基因型的多樣性分離外，環境條件的影響可能也是重要因素。

瑞典學者H.尼爾松－埃赫勒根據小麥粒色的遺傳，首先提出解釋數量性狀遺傳的多基因假說。其後經美國學者E.M.伊斯特和R.A.埃默森根據玉米果穗長度和煙草花冠長度的遺傳試驗結果，對多基因假說作了補充。多基因假說認為：同一數量性狀的遺傳受為數甚多的基因支配；各個基因對性狀的作用都很微小(英國K.馬瑟稱之為多基因或微效多基因);這些基因彼此間沒有顯隱性關係，而其作用一般是累加的，稱為加性效應；其遺傳行為也服從孟德爾遺傳規律和連鎖遺傳規律。

實際上決定數量性狀遺傳的基因並非都是加性效應，所以在許多場合會出現與上述情況不同的特點。F1可能偏向於某親本或與某親本相近，甚至超過雙親;F2群體呈現偏態分佈。這是由於決定這一類數量性狀遺傳的基因除具有加性效應外，還具有顯性效應和上位性效應。上位性效應指控制該數量性狀遺傳的非等位基因間所發生相互作用。它和顯性效應統稱為非加性效應。

數量性狀遺傳的研究對象是群體。需藉助數理統計方法，對群體進行抽樣測定和統計分析，獲得某些參數，從而闡明數量性狀的遺傳變異動態與特點。數量性狀遺傳常用的遺傳參數主要有5類:①遺傳力。即某一性狀的表型方差(或表型變異量)中遺傳成分所佔的比重。②配合力。即兩個親本(純系、自交系或品種)材料雜交后，在雜種後代的產量或其他性狀表現中所起作用相對大小的度量。③遺傳相關。指同一遺傳材料中兩個性狀間由於遺傳原因所體現的相關，即這個性狀基因型值間的相關。④遺傳進度。又稱遺傳獲得量。即在一定選擇強度下，從原來群體中選出的後代的某性狀平均值比原群體平均值提高的數值。預期的遺傳進度(△G)是選擇差（i，選擇前和選擇後上下代兩個平均值的差數）和性狀遺傳力(h)的函數，即△G=ih。i為絕對值，受表型標準差(σp)的影響。為使之標準化，以便比較不同性狀和不同群體的選擇效果，可將上式兩邊均除以σp，得是相對值，可寫為k,稱為選擇強度。這樣遺傳進度。如為廣義遺傳力,；如有狹義遺傳力，則。測定遺傳進度可以估計對某性狀的選擇效果。⑤選擇指數。一種綜合選擇的指標。即把選擇的目標性狀擴大到與該主要性狀有較密切關係的一些性狀，對每個性狀都按其相對經濟重要性和不同性狀間的表型相關與遺傳相關，通過多元統計方法進行適當加權，形成如下的線性關係： 。

式中x1、x2、x3、…、xn為各性狀的表型值；b1、b2、b3、…、bn為相應性狀的加權係數;I是選擇指數。選擇時，計算供試株系或單株的選擇指數，按其數值大小作為去留標準。這樣，根據多個性狀進行綜合選擇，有助於使目標性狀獲得最大的改進。