路易斯結構式
以吉爾伯特·路易斯命名的結構式
路易斯結構(Lewis structures,又稱做Lewis 點圖像, 電子點圖像,Lewis 電子點式,Lewis 點結構,和電子點結構)是分子中原子和原子鍵結構標示孤對電子存在的圖像,以美國物理化學家吉爾伯特·路易斯(Gilbert Newton Lewis)的名字命名。
19世紀的化學家們創造了用元素符號加畫短棍“—”的形式來表明原子之間按“化學價”相互結合的結構式,原子間用“—”相連表示用了“1”價,如水的結構式為H-O-H;用“=”相連表示互用了“2價”,如二氧化碳的結構式為O=C=O,用“≡”相連則表示互用了“3價”,如氰化氫H-C≡N中的C≡N。
當時已經知道,在絕大多數情況下,氫總是呈1價,氧總是呈2價,氮總是呈3或5價,鹵素則在有機物中大多呈1價,在無機物中除呈1價,還呈3、5、7價,等等。這種“化合價”概念是由英國化學家弗蘭克蘭[Frankland Edward(1825-1899)]在1850年左右提出的。他總結了化合物中原子個數比的規律,並為元素周期性的發現做了鋪墊——元素化合價並無正負之分,同種原子的分子,例如,H2其中的氫也呈1價,故氫分子的結構式為H-H。
半個多世紀后的20世紀初,美國化學家路易斯[Gilbert Newton Lewis,(1875-1946)]把弗蘭克蘭結構式中的“短棍”解釋為兩個原子各取一個電子配成對,即:“—”是一對共用電子,“=”是2對共用電子,“≡”是3對共用電子對。換句話說,經典的弗蘭克蘭化合價被解釋為原子能夠提供來形成共用原子對的電子數。路易斯還認為,稀有氣體最外層電子構型(8e-)是一種穩定構型,其他原子傾向於共用電子而使它們的最外層轉化為稀有氣體的8電子穩定構型——八隅律。路易斯又把用“共用電子對”維繫的化學作用力稱為共價鍵。後人稱這種觀念為路易斯共價鍵理論。
“—”表示共用一對電子。
“=”表示共用兩對電子。
“≡”表示共用三對電子。
弗蘭克蘭的“化合價”=Lewis的電子共用電子對數目。
① 柯賽爾的“八隅律”
認為稀有氣體的8e外層是一種穩定構型。
其它原子傾向於共用電子而使其外層達到8e外層。
如:
② 成鍵電子與孤對電子的表示
成鍵電子=鍵合電子——指形成共價鍵的電子。
孤對電子——指沒有參與化合鍵形成的電子。
③ 結構式的表示:
鍵合電子——用線連
孤對電子——用小黑點
如:
④ Lewis電子結構式的局限性
按柯賽爾的“八隅律”規則,許多分子的中心原子周圍超出8e但仍然穩定。
如: PCl5 BCl3 B周圍5個e的 共振結構
要正確寫出共振結構式,應符合下列幾條規則:
① 共振結構式之間只允許鍵和電子的移動,而不允許原子核位置的改變。
② 所有的共振結構式必須符合Lewis結構式。
③ 所有的共振結構式必須具有相同數目的未成對電子。以烯丙遊離基為例:。
④ 電子離域化往往能夠使分子更為穩定,具有較低的內能,為了衡量這種穩定性,可以使用共振能。所謂共振能就是實際分子的能量和可能的最穩定的共振結構的能量之差,以苯分子為例。共振結構中,共價鍵數目越多的,能量越低,越穩定,它在雜化體中所佔幾率較大。苯的真實結構是由八種結構式共振形成的共振雜化體,應該指出,在上例中各式都應是在一個平面上的正六邊形碳環,不可以有任何變化,這些共振結構式實際上都是假設的結構,它們之間的不同,僅在於電子分佈情況同。因此,各共振式的能量不全相同。I和II式結構相似,能量最低,其餘共振式的能量都比較高,能量最低而結構又相似的共振式在真實結構中參與最多,或稱貢獻最大,因此,可以說苯的真實結構主要是I式和II式的共振雜化體。
⑤ 結構式中所有的原子都具有完整的價電子層都是較為穩定的。
⑥ 有電荷分離的穩定性較低。
⑦ 負電荷在電負性較大的原子上的較穩定。
共振效應是共軛效應的繼續和發展,共振效應也包括共軛效應和超共軛效應。它們都是一個取代基通過π電子系統的報化效應,在很多情況下,誘導效應和共振效應往往同時起作用,所以也常合併稱為電子效應,但是它們不是一個東西。
共振論的應用主要包括說明有機化合物的物理性質和化學性質兩個方面,在物理性質方面可以用來說明分子的極性(偶極矩)鍵長,離域鍵、鍵能等,在化學性質方面可以用來預測反應的產物比較化合物酸鹼性的強弱;判斷反應條件穩定,電荷的分佈位置和解釋多重反應性能等,但只應當適當選用而不能過分強調它的應用。總之,任何一個化學反應是電子云的分佈價鍵的變化和共振的結果所以解釋絕大多數化學或立體化學問題時共振論,共價鍵論(價鍵和分子軌道理論)量子力學等理論要結合起來,要確實掌握共振的定量概念,因為,它們相互補充也有它們的缺點,屬於共扼效應有一些問題,也是要運用分子軌道理論方法來解決。用共振式來形式化地(定性地)描述電子離域化系統很方便,在實際用上很有價值,因此用仍很廣泛
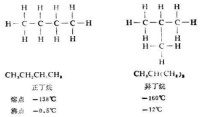
路易斯結構式