abc猜想
abc猜想
數論中的abc猜想(亦以Oesterlé–Masser猜想 而聞名)最先由喬瑟夫·奧斯達利(Joseph Oesterlé)及大衛·馬瑟(David Masser)在1985年提出,2012年數學家望月新一聲稱證明了此猜想,目前正在核查中。數學家用三個相關的正整數a,b和c(滿足a + b = c)聲明此猜想(也因此得名abc猜想)。若d是abc不同素因數的乘積,這個猜想本質上是要說d通常不會比c小太多。換句話來說,如果a,b的因數中有某些素數的高冪次,那c通常就不會被素數的高冪次整除。
abc猜想因它所帶來的一些關於數論的有趣的結論而著名,很多著名的猜想和定理都緊接著abc猜想問世。數學家Goldfeld (1996)認為abc猜想是“the most important unsolved problem in Diophantine analysis”。
Lucien Szpiro(法國數學家,因其在數論、算術代數幾何和交換代數上的貢獻而知其名)在2007年時嘗試攻克此猜想,但后被證明其中有誤。在2012年8月,日本的京都大學數學家望月新一(mochizuki shin'ichi)發布了其四篇預印文稿,介紹了他的Inter-universal Teichmüller theory(全面一般化泰希米勒理論),並聲稱用此理論可證明包括abc猜想在內的幾個著名猜想。他的論文在數學期刊上刊登以供參考查閱,很多人也開始學習他的理論。很多數學家對他的文章持懷疑態度,也正是因為他這篇古怪晦澀的證明,我們知道了,要解決這個猜想或許還是要走上孤獨的漫漫長路。不變的是,在我們試證明其正誤之時,數學水平得到提高,也終將找到解決abc猜想之路。
在我們詳細介紹這個猜想之前,先來說一說整數的根數(radical):∀n∈N ,其所有不同素因子(prime factor)的乘積為根數(1的根數為1),記為:rad(n)。舉例說明:
rad(16) = rad(2) = 2,
rad(17) = 17,
rad(18) = rad(2 ⋅ 3) = 2 · 3 =6 ,
rad(1000000) = rad(2 ⋅ 5) = 2 ⋅ 5 = 10。
若a,b和c是滿足a+b=c的互素正整數,通常有c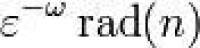 取代,其中ω是a,b,c的不同質因子的數目。
取代,其中ω是a,b,c的不同質因子的數目。
abc猜想(abcconjecture):∀ε>0,僅存在有限多的三元組(a,b,c)滿足a、b、c是互素正整數,a+b=c,而且
還有一些等價的形式,
abc猜想Ⅱ:∀ε>0,∃Kε,使任意滿足a、b、c為互素正整數,a+b=c的三元組(a,b,c)也同時滿足
第三種定義涉及了三元組(a,b,c)的質量(quality)q(a,b,c):
看幾個例子:
q(4, 127, 131) = log(131) / log(rad(4·127·131)) = log(131) / log(2·127·131) = 0.46820...
q(3, 125, 128) = log(128) / log(rad(3·125·128)) = log(128) / log(30) = 1.426565...
我們知道,對於一般滿足a、b、c為互素正整數,a+b=c的三元組(a,b,c),有c < rad(abc),此時,
q(a,b,c) < 1,而q>1之情況實屬少見,此時這些數的因數中存在著小素數的高次冪。
abc猜想Ⅲ:∀ε>0,僅存在有限多的三元組(a,b,c)滿足a、b、c是互素正整數,a+b=c,而且
已知存在無限多的三元組(a,b,c)滿足a、b、c是互素正整數,a+b=c,而且q(a,b,c)> 1,然而(這個猜想想要表述的就是),在q>1.01,q>1.001,q>1.0001甚至q離1更近時,三元組卻是有限多的。要特別說明的是,如果這個猜想是真的,必存在一個三元組(a,b,c)使q取到最大值。
1996年,愛倫·貝克提出一個較為精確的猜想,將rad(n)用
abc猜想
abc猜想將許多丟番圖問題都包含在其中,比如費馬大定理。同許多丟番圖問題一樣,abc猜想完全是一個素數之間關係的問題。斯坦福大學布拉恩·康拉德(Brian Conrad)曾說,“在a、b和a+b的素數因子之間存在著更深層的關聯”。
條件ε > 0再此是必要的,因為滿足rad(abc)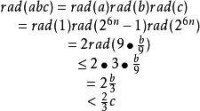 b
b
首先我們指出,b可以被9整除:
依據這個事實,我們得到:
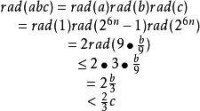
abc猜想
當用另一指數替換6n致使b有很大的平方因子,根數與c之間的比率可以任意小。當p是大於2的素數時:
同樣地,b可以被p 整除:
我們再一次得到了相似的結果:
下面將給出一組高質量的三元組(其中c的根數相對來說很小);這個三元組質量為1.6299,這是Eric Reyssat(Lando & Zvonkin 2004, p.137)發現的。
a = 2,
b = 3 ·109 = 6,436,341,
c = 23 = 6,436,343,
rad(abc) = 15042。
ABC@home 是一個由荷蘭的一個數學研究院 Mathematical Institute of Leiden University 運作的,基於 BOINC 分散式計算平台的數學類項目,旨在通過搜索滿足ABC猜想條件的三元數組獲得這些數組的分佈從而幫助數學家解決這個猜想。
即它利用分散式計算窮舉直到 c<=10的滿足ABC猜想條件的 (a,b,c) 三元數組,也就是說滿足要求 c=a+b, a
 2012年8月,日本京都大學數學家Shinichi Mochizuki(望月新一)公布了 有關abc猜想(abc conjecture)長達500頁的證明。雖然尚未被證實整個證明過程是正確無誤的,但包括陶哲軒在內的一些著名數學家均對此給出了正面評價。
2012年8月,日本京都大學數學家Shinichi Mochizuki(望月新一)公布了 有關abc猜想(abc conjecture)長達500頁的證明。雖然尚未被證實整個證明過程是正確無誤的,但包括陶哲軒在內的一些著名數學家均對此給出了正面評價。
 美國哥倫比亞大學數學家Dorian Goldfeld評價說:“abc猜想如果被證明,將一舉解決許多著名的Diophantine問題,包括費馬大定理。如果Mochizuki的證明是正確的,這將是21世紀最令人震驚的數學成就之一。”
美國哥倫比亞大學數學家Dorian Goldfeld評價說:“abc猜想如果被證明,將一舉解決許多著名的Diophantine問題,包括費馬大定理。如果Mochizuki的證明是正確的,這將是21世紀最令人震驚的數學成就之一。”
項目通過研究這些三元數組的分佈,試圖尋找證明ABC猜想這個數學未解問題的方法。如果證明了ABC猜想,就可以部分證明費馬-卡特蘭 (Fermat-Catalan) 猜想,完全證明 Schinzel-Tijdeman 猜想等等。ABC猜想的具體內容是:對於所有e>0,存在與e有關的常數C(e),對於所有滿足a+b=c,a與b互質的三正整數組(a,b,c),均成立 c<=C(e)((rad(abc))^(1+e))。支持ABC猜想的證據有很多,比如說ABC猜想的多項式版本成立,ABC猜想也蘊含了費馬大定理。D. Goldfeld 評價ABC猜想為“丟番圖分析(意即係數與解均為整數的方程的分析)領域中最重要的未解決問題”。 ABC@home 希望能夠通過了解滿足條件的三元數組的分佈來協助數學家解決ABC猜想。
許多數學家都花費了大量的精力試圖證明這一猜想。在2007年,在法國數學家呂西安·施皮羅(Lucien Szpiro)在1978年的研究工作的基礎之上,首次宣布對abc猜想的證明,但很快就發現證明中存在著缺陷。
2006年,荷蘭萊頓大學數學系和荷蘭Kennislink科學研究所聯合啟動了一個BOINC項目名為“ABC@Home”,用以研究該猜想。

日本數學家望月新一

望月論文中的定義和數論中傳統概念的比較
望月新一的研究工作與前人的努力並沒有太多關聯。他建立了一套全新的數學方法,使用了一些全新的數學“對象”——這些抽象實體可類比為我們比較熟悉的幾何對象、集合、排列、拓撲和矩陣,只有極少的數學家能夠完全理解。就如同戈德費爾德所說:“在當今,他或許是唯一一個完全掌握這套方法的人。”
康拉德認為,這項研究工作“包含著大量的深刻思想,數學界要想完全理解消化需要花很長的時間”。整個證明包含四個長篇論文,每一篇都是建立在之前論文的基礎上。“需要花費大量的時間來研讀並理解這些深奧的長篇證明,所以我們不能僅僅關注此證明的重要性,更重要的是沿著作者的證明思路進行研究。”
望月新一取得的研究成果使得這一切努力都是值得的。康拉德說:“望月新一曾經成功證明過極為艱深的定理,並且他的論文表達嚴謹,論述周密。這些都使我們對於成功證明abc猜想充滿了信心。”另外,他還補充道,所取得的成績並不僅限於對此證明的確認。“令人感到興奮的原因不僅僅在於abc猜想或許已被解決,更在於他所使用的方法和思想將會成為以後解決數論問題的有力工具。”
歷史上反直覺的卻又被驗證為正確的理論,數不勝數。一旦反直覺的理論被證實是正確的,基本上都改變了科學發展的進程。舉一個例子:牛頓力學的慣性定律,物體若不受外力就會保持當前的運動狀態,這在17世紀無疑是一個重量級的思想炸彈。“物體不受力當然會從運動變為停止”,這是當時的普通人基於每天的經驗得出的正常思想。而實際上,這種想法,在任何一個於20世紀學習過初中物理、知道有種力叫摩擦力的人來看,都會顯得過於幼稚。但對於當時的人們來說,慣性定理的確是相當違反人類常識的!
ABC猜想之於數論研究者,就好比牛頓慣性定律之於17世紀的普通人,更是違反數學上的常識。這一常識就是:“a和b的質因子與它們之和的質因子,應該沒有任何聯繫。”原因之一就是,允許加法和乘法在代數上交互,會產生無限可能和不可解問題,比如關於丟番圖方程統一方法論的希爾伯特第十問題,早就被證明是不可能的。如果ABC猜想被證明是正確的,那麼加法、乘法和質數之間,一定存在人類已知數學理論從未觸及過的神秘關聯。
目錄
