共找到2條詞條名為駐點的結果 展開
- 數學概念之一
- 漢語詞語
駐點
數學概念之一
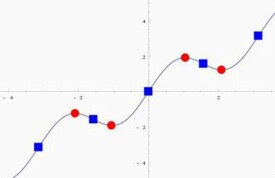
在微積分,駐點(StationaryPoint)又稱為平穩點、穩定點或臨界點(CriticalPoint)是函數的一階導數為零,即在“這一點”,函數的輸出值停止增加或減少。對於一維函數的圖像,駐點的切線平行於x軸。對於二維函數的圖像,駐點的切平面平行於xy平面。值得注意的是,一個函數的駐點不一定是這個函數的極值點(考慮到這一點左右一階導數符號不改變的情況);反過來,在某設定區域內,一個函數的極值點也不一定是這個函數的駐點(考慮到邊界條件),駐點(紅色)與拐點(藍色),這圖像的駐點都是局部極大值或局部極小值。
駐點並不是點,而是和極值點相似,代表著這一點的x值。
因此,駐點不一定是極值點,極值點也不一定是駐點。
函數的一階導數為0的點(駐點也稱為穩定點,臨界點)。對於多元函數,駐點是所有一階偏導數都為零的點。
函數的平穩點的術語可能會與函數圖的給定投影的臨界點相混淆。
“臨界點”更為通用:功能的平穩點對應於平行於x軸的投影的圖形的臨界點。另一方面,平行於y軸的投影圖的關鍵點是導數不被定義的點(更準確地趨向於無窮大)。因此,有些作者將這些預測的關鍵點稱為“關鍵點”。
拐點是導數符號發生變化的點。拐點點可以是相對最大值或相對最小值(也稱為局部最小值和最大值)。如果函數是可微分的,那麼拐點是一個固定點;然而並不是所有的固定點都是拐點。如果函數是兩次可微分的,則不轉動點的固定點是水平拐點。例如,函數x^3在x=0處有一個固定點,也是拐點,但不是轉折點。
在駐點處的單調性可能改變,在拐點處單調性也可能改變,凹凸性一定改變。
拐點:使函數凹凸性改變的點。
駐點:一階導數為零。
可導函數的極值點一定是它的駐點,不可導的點可以是極值點,但它不是駐點。但反過來,函數的駐點【不一定】是極值點.(同濟六版155頁中間)
函數
2.