相平面法
相平面法
相平面法:是 Poincare. H 於1885年首先提出來的,它是求解一、二階線性或非線性系統的一種圖解法,可以用來分析系統的穩定性。
目錄
用繪製在直角平面坐標上的表徵變數及其變化速率間關係的軌跡來研究二階自治系統的一種圖解方法。這種方法可用來分析一大類非線性系統的運動。自治系統是指其運動方程中不顯含時間變數t的系統。二階自治系統運動方程的一般形式為
式中黑點表示變數對時間t求導數。如果x表示位移,則凧和尦就是速度和加速度。在運用相平面法分析時,以x為橫坐標、以為縱坐標構成相平面,並將自治系統運動方程化成相應的相軌跡方程,它是如下形式的一階微分方程:
通過解析的方法或近似計算方法來求解相軌跡方程,即可得到相軌跡方程解的表達式或數值解,它在相平面上的圖形稱為相軌跡。對於系統不同的初始條件,可畫出不同的相軌跡,它們全體組成系統的相軌跡族(圖1)。在相平面上,根據相軌跡族能明顯地看出系統的各種全局性質。例如,運動類型,穩定性,極限環和奇點(系統的靜平衡點)的位置,數目和類型等。因此,相平面圖能相當全面地刻劃二階自治系統的運動特性。
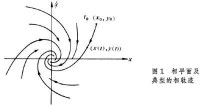
相平面法
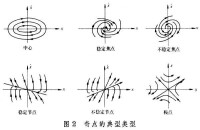
相平面法

相平面法
如果能得到相軌跡方程解的顯表達式,則二階自治系統的相軌跡可精確繪出。否則,只能根據相軌跡的一些基本性質,採用近似方法來繪製相軌跡。在這類近似繪圖法中最常用的有等傾線法、里耶納德法等。相平面法在用於分析繼電控制系統時尤為簡單和方便。
對於相軌跡方程為