正射校正

正射校正是對影像進行幾何畸變糾正的一個過程，它將對由地形、相機幾何特性以及與感測器相關的誤差所造成的明顯的幾何畸變進行處理。輸出的正射校正影像將是正射的平面真實影像。

許多用戶都要對他們的影像進行正射校正。這是因為，他們的影像需要非常精確的定位精度，或者整個影像都必須採用統一精度比例。例如，進行正射校正後，就能夠對影像進行測量，或者在影像中精確地定位某些特徵、採集供GIS使用的信息，或者將影像同其他精確校正影像結合起來，進行進一步複雜的分析。

從攝影測量的角度，衛星遙感影像可以看作是一個中心投影的結果，它必然會受到感測器觀測角度和地面高 程的影響，特別是在影像的邊緣，地面高程引起的視差更是不可忽視。在圖1中，從衛星S看到的地面點M，其坐標應為X；但是按照正向模型的計算，求得的坐標則為X'。這裡，由於高程h的影響，正向模型的計算誤將X'當作是M的地面坐標，而距離IX-X’l是由於高程h引起的視差。以LANDSAT衛星為例，當，h=1000m時，在影像邊緣附近引起的視差大約是130m，約合4個像元。

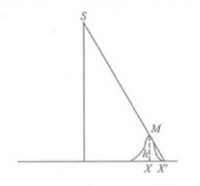
正射校正的目的就是要消除這種由地面高程引起的視差，在數字高程模型(Digital Elevation Model，DEM)的幫助下，得到M點正確的位置坐標X。

在正向模型計算時，得到地面坐標X'的高程h‘’很容易，但得到M點即坐標X的高程h卻很難。為此，在工程實現中採用了迭代演演算法的方式來求得M點的坐標X。

正射校正可以選擇的方法很多，主要包括嚴格物理模型和通用經驗模型兩種。嚴格物理模型以共線方程為代表，但是為獲得較高的精度需要已知感測器的軌道參數和姿態參數等；經驗模型應用靈活，只要有足夠數量的控制點就可以獲得正射影像，但是其精度往往受到地形和控制點的限制。最主要的正射影像製作主要是基於立體像對的數字攝影測量方法。但立體像對遙感影像獲取不易、成本較高，而且需要一定數量的控制點。這裡主要介紹幾種常見的正射校正演演算法，及如何在軟體中實現正射校正。

1．共線方程模型

共線方程是攝影測量里最基本的公式，是研究最多和使用最廣的空間幾何模型。共線方程校正法是建立在對感測器成像時的位置和姿態進行模擬和解算的基礎上的。由於其嚴格給出了成像瞬間物方空間和像方空間的幾何對應關係，所以其幾何校正精度是認為最高的。共線方程模型的應用分兩種情況：軌道參數及姿態參數已知和未知。的商業軟體中基本都以此為基礎實現各種來源的遙感影像糾正功能。正因為共線方程模型的嚴密特性，因此它在各種解析度的遙感影像糾正中都適用。對共線方程的研究主要是關於其解算方位元素過程由誤差方程病態所引起的解算結果並非最優問題。對此提出的演演算法很多，如增加虛擬誤差方程、合併相關項、嶺估計方法、阻尼最小二乘法、線性規劃法、中心標準化方法等，雖然這些解算方法在諸多的研究文獻中很難達到滿意的效果，但是其精度在正射校正中完全能夠滿足應用要求。而在CCD感測器的共線方程模型解算當中，應用最多的是嶺估計方法。

2．基於仿射變換的嚴格幾何模型

高解析度遙感影像的研究與應用已經成為了遙感應用研究的熱點問題。圍繞高解析度遙感影像的處理，出現了許多關於新型感測器的成像機理、圖像三維處理及測圖技術等。基於仿射變換的感測器模型和有理函數模型是其中的典型代表。

高解析度衛星感測器的突出特徵是長焦距和窄視場角，大量實驗證明，這種成像幾何關係如果用共線方程來描述將導致定向參數之間存在很強的相關性，從而影響定向的精度和穩定性。Okamoto提出了一種基於仿射投影模型的方法，Hatlori與Ono進一步研究與應用了該模型。

3．改進型多項式模型

改進型多項式的感測器模型是一種簡單的通用成像感測器模型，其原理直觀明了，並且計算較為簡單，特別是對地面相對平坦的情況，具有較好的精度。這種方法的基本思想是迴避成像的幾何過程，而直接對影像的變形本身進行數學模擬、把遙感圖像的總體變形看做是平移、縮放、旋轉、偏扭、彎曲，以及更高次的基本變形綜合作用的結果。

4．有理函數模型

有理函數模型(RFM)在近年來才受到普遍關注，特別是IKONOS衛星的成功發射推動了對有理函數的全面研究，國際攝影測量與遙感協會成立了專門工作組研究有關RFM的校正精度、穩定性等各方面問題，Tao和Dowman等對其進行了系統的研究與比較。有理函數模型是各種感測器幾何模型的一種更廣義的表達形式，是對不同的感測器模型更為精確的表達形式。它能適用於各類感測器，包括最新的航空和航天感測器。它的缺點是模型解算複雜，運算量大，並且要求控制點數目相對較多；但其優點是由於引入較多定向參數，模擬精度很高。