共找到3條詞條名為視差的結果 展開
- 視覺名詞
- [美]布魯斯·卡明斯所著書籍
- 手機遊戲
視差
視覺名詞
視差就是從有一定距離的兩個點上觀察同一個目標所產生的方向差異。從目標看兩個點之間的夾角,叫做這兩個點的視差角,兩點之間的連線稱作基線。只要知道視差角度和基線長度,就可以計算出目標和觀測者之間的距離。

視差映射技術
觀測者在兩個不同位置看同一物體的方向之差。比如,當你伸出一個手指放在眼前,先閉上右眼,用左眼看它;再閉上左眼,用右眼看它,會發現手指相對遠方的物體的位置有了變化,這就是從不同角度去看同一點的視差。視差可用觀測者的兩個不同位置之間的距離(基線)在天體處的張角來表示。
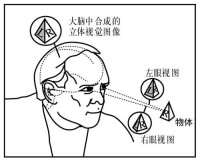
簡單的視差例子
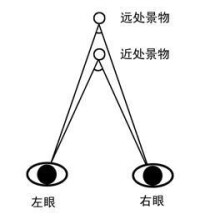
遠近視差
⑵視差產生的原因:由於度量標尺(分划板)與被測物體(像)不共面,使得當眼睛晃動(觀察位置稍微改變)時,標尺與被測物體之間會有相對移動。
視差就是指你所見到的物體與物體的客觀形態有一定差距。
消除的辦法就是調整目鏡(也就是對焦),一直調整到眼睛在目鏡中上下移動,而目鏡中的十字絲一直都是重合的,不會出現影像。
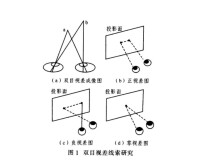
雙目視差線研究
消視差的方法:若待測像與標尺(分划板)之間有視差時,說明兩者不共面,應稍稍調節像或標尺(分划板)的位置,並同時微微左右或上下晃動頭部,做到不管眼睛離瞄準具的遠近、左右、上下,瞄準線看來一直會是固定在目標上的同一點,直到待測像與標尺之間無相對移動,即無視差。
為了準確定位和測量,必須把像與叉絲或分划板標尺調到一個平面上,即作消視差調節。例如,用直尺直接測量長度,尺和物必須緊貼才能使測量和讀數準確。
精度較高的儀錶,其指針與標尺之間總會有一段小距離,應盡量在正視位置進行讀數。有些錶盤上安裝平面鏡,用以引導正確的視點位置,眼睛、指針、指針象三點一線,從而減小視差,使讀數更準確。有視差時,若眼睛沒有保持在中心位置,瞄準點可能會有偏差。
坐火車時,會感到大地瞬間旋轉,是因為人的視覺有解析度(0.17s)而圖像變換太快,大腦處理時我們會
感到圖片連接起來了,大地就會瞬間旋轉(坐火車時在平原會感到這種情況)
測量天體視差是確定天體之間距離最基本的方法。觀測者在兩個不同位置看到同一天體的方向之差。視差可以用觀測者的兩個不同位置之間的距離(又稱基線)在天體處的張角來表示。
天體的視差與天體到觀測者的距離之間存在著簡單的三角關係。測出天體的視差,就可以確定天體的距離。因此,天體的視差測量是確定天體距離的最基本的方法,稱為三角視差法。由於天體的距離都很遙遠,它們的視差很小,為精確測定它們的視差,必須儘可能地把基線拉長。在測定太陽系內一些天體的視差時,以地球的半徑作為基線,所測定的視差稱為周日視差。在測定恆星的視差時,以地球和太陽之間的平均距離作為基線,所測定的視差稱為周年視差。
視差
它的定義是:通過M點的地球半徑在天體S處的張角。(如圖)
周日視差隨著天體的高度變化而改變。當天體位於天頂Z時,它的周日視差為零;當天體位於地平時,它的周日視差達到極大值P0,稱為周日地平視差。周日地平視差P0和地心到天體的距離D以及地球半徑R之間的關係可以表示為:

視差公式
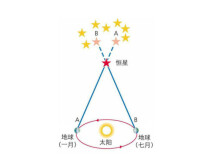
三角視差法
是地球繞太陽周年運動所產生的視差。它的定義是:地球和太陽間的距離在恆星處的張角。恆星的周年視差π與太陽到恆星的距離r以及地球到太陽的平均距離α之間的關係(圖2)可以表示為:
恆星的周年視差π都小於一角秒,所以通常π以角秒為單位,並把上式寫為:

圖公式三
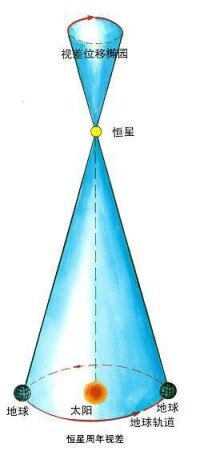
恆星周年視差
已知α和π,便可求得r。
自哥白尼提出日心地動學說(見日心體系)以後的近三百年間,許多人企圖發現恆星的周年視差,但都沒有成功,以致有些人對哥白尼學說的正確性持懷疑態度,其中包括丹麥著名天文學家第谷。直到1837~1839年,俄國В.Я.斯特魯維、德國貝塞耳和英國T.亨德森才分別測出了織女星(即天琴座α)、天鵝座61和南門二(即半人馬座α)三顆近距恆星的周年視差。早期用目視法測定恆星的周年視差,精度不高。二十世紀以來,開始使用口徑大、焦距長的大型折射或反射望遠鏡和照相方法測定視差。當恆星同地球的距離等於100秒差距時,其周年視差的觀測誤差已相當於其視差本身相等的數值,因此只有對距離小於100秒差距的近距星,才能比較準確地測定它們的三角視差。美國耶魯大學天文台在1952年出版的《恆星視差總表》中列出了約 6,000顆恆星的三角視差。近二、三十年來又測定了百分之十以上的暗星的三角視差。例如在1969年版《格利澤星表》中,列出了1,049顆距離在20秒差距之內的近距星的視差。在全天恆星中,南門二的一顆伴星的視差最大,等於0獎76,故有比鄰星之稱。
是太陽在空間運動所產生的視差(也稱視差動)。長期視差πS和太陽到恆星的距離r以及太陽在一年裡所走過的距離d之間的關係(圖3)可以表示為:
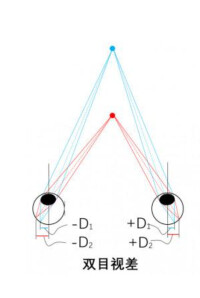
雙目視差
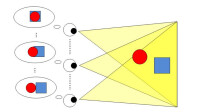
運動視覺差
恆星的距離遙遠,πS十分小,所以當它以角秒計時:。
太陽對於鄰近恆星的空間速度V⊙=19.7公里/秒,因此,太陽附近恆星的長期視差等於其周年視差的4.15倍。對於具有某種共同特徵的一組星,如視星等或光譜型在某一確定範圍內的恆星,或某種類型的變星等,可利用自行或視向速度的觀測數據進行統計分析,求出它們的長期視差。
人們早就知道,雙眼視覺具有對方向和深度進行信息加工的特殊功能。眼睛的視網膜是平面的(視網膜是眼光學系統的成像屏幕,它是一凹形的球面),卻能產生三維空間的知覺。
高級動物的視覺可分為兩大類。雙眼在頭部兩側的哺乳動物,如兔,兩眼的視野完全不同。左眼和右眼分別感受頭部左側和右側的光刺激,因此只有單眼視覺。人和靈長類動物,如猴,雙眼都在頭的前部,絕大部分視野重疊,左右眼可同時接受同一物體的光刺激,因而具有雙眼視覺的功能。雙眼視覺可以彌補視野中存在盲點的缺陷,又擴大了平面視野,對立體視覺的形成以及通過視覺判斷物體的遠近距離起著重要作用。
人類通過雙眼視覺判斷距離的能力叫作深度知覺。它包括兩種情況。一種是判斷觀察者到物體的距離,也稱為絕對距離。另一種是判斷兩個物體之間的距離,或者同一物體內部不同部分之間的距離,又稱為相對距離。實驗表明,人判斷相對距離的能力比判斷絕對距離的能力要精確許多倍。
在我們眼球的視網膜中央密集著大量的錐體細胞,呈黃色,叫黃斑。黃斑中央有一小凹,叫中央窩,它具有最敏銳的視覺。在觀看一個物體時,兩隻眼睛要同時對準這個物體,即雙眼視軸向鼻側集中,從而使兩眼的中央窩對準物體,獲得清晰的視象。這種現象叫雙眼視軸的輻合。看近距離物體時,雙眼的輻合角度增大,視軸趨於集中;看遠距離物體時,雙眼的輻合角度減小,視軸趨於分散;觀察更遠的物體時,視軸接近平行。圖一表明,視軸的輻合角度Q取決於觀察者的目間距d和物體P離開眼睛的距離L,即Q=d/L。顯然,目間距大的人對距離知覺的準確性有利。當物體的距離非常遠,L接近∞時,距離再有變化,輻合角度的變化就很小了。這時輻合機制在距離知覺中基本上不再起作用。人依靠輻合所提供的信息能相當準確地判斷45米範圍內物體的距離。
看一個平面物體時,物體的視象分別落在兩眼視網膜的對應部位上。圖二中,如果注視點為Z,則Z點的象便落在兩眼視網膜的中央窩Z1和Z2處。物體上x和y點的視象也分別落在兩眼視網膜的對應部位x1、x2、y1、y2處。即y1z1=y2z2,z1x1=z2x2。物體的其他部分的視象也同樣落在兩個視網膜各自的對應部位上。可以想象,如果把兩個視網膜重合起來,兩個視象是完全重疊的。這時人知覺到的便是平面物體。
在看立體物體時,由於人的兩眼之間相距大約65毫米,所以兩眼是從不同角度觀察的:除兩眼能看到的物體的共同部分外,左眼看到物體的左邊部分多些;右眼看到物體的右邊部分多些。如圖三所示,如果注視點為Z,這時y1z1不等於y2z2,z1x1也不等於z2x2。此時如果把兩眼的視網膜重疊起來,則兩個視象在中央窩及其附近是重合的,其餘部分卻不完全重合。因此在左眼和右眼視網膜上分別感受著不完全相同的刺激,從而產生了雙眼視網膜的視象差,簡稱為雙眼視差。雙眼視差所引起的神經衝動傳送到大腦,經大腦皮質視區的綜合作用便形成一個單一的,具有立體感的視覺影象,形成立體知覺。在觀看相隔一定距離的兩個物體時,不但能感知到它們之間的前後關係,還能判斷它們相隔的距離,這就是深度知覺。可見,雙眼視差是立體視覺和深度知覺的基礎。蒙上一隻眼就不容易看出物體的厚度,用單眼穿針引線不如雙眼方便,就是這個道理。
恆星視差
解題過程

視差

視差

運動視差
遠恆星的絕對星等,進而求出距離。造父變星是一種性質非常奇特的恆星。所謂變星是指光度周期性變化的恆星。造
父變星的獨特之處就在於它的光變周期和絕對星等有一個特定的關係(稱為周光關係)。通過觀測光變周期就可以得出造父變星的絕對星等。有了絕對星等,一切也就好 說了 造父變星有兩種:經典造父變星和室女座W型造父變星,它們有不同的周光關係。天琴座的RR型變星也具有特定的周光關係,因此也可以用來測定距離。這種使用變 星測距的方法大致可以測量108秒差距的恆星。
人們觀測到,更加遙遠的恆星的光譜都有紅移的現象,也就是說,恆星的光譜整個向紅端移動。造成這種現象的原因是:遙遠的恆星正在快速的離開我們。根據多普勒效應可以知道,離我們而去的物體發出的光的頻率會變低。
1929年,哈勃(Hubble,E.P.)提出了著名的哈勃定律,即河外星系的視向退行 速度和距離成正比:v=HD.這樣,通過紅移量我們可以知道星體的推行速度,如果哈勃常數H確定,那麼距離也就確定了(事實上,哈勃太空望遠鏡的一項主要任務就是確定
哈勃常數H)。這樣,我們就可以測量到這個可觀測宇宙的邊緣了。
不過還是有一個問題,這種天文學的測量如同一級一級的金字塔,那麼金字塔的地基——天文單位到底是多少呢?如果測量不出天文單位,其他的測量就都成了空中樓閣 天文單位的確是天文測量的基石。20世紀60年代以前,天文單位也是用三角測量法測出的,在這之後,科學家使用雷達測量日-地距離。雷達回波可以很準確的告訴我們太陽里我們有多遠,這樣一來,天文學家就可以大 膽的測量遙遠的星辰了。

視差
視差法是一種比較容易理解的距離測量技術。你可以自己來體驗一下:舉起你的一個手指放在鼻子前幾厘米處,睜著左眼閉起右眼觀察手指在背景中的位置;然後閉上左眼睜開右眼,你會發現手指在你面前移動了一段距離。實際上並不是手指移動了,而是因為觀察的角度改變了的緣故。這種視運動就叫做視差。“這同測量恆星的距離有什麼關係?”不要著急,把你的同一個手指放在你面前30厘米處,重複剛才的實驗,你將發現由於視差而產生的手指位移大大減少了。也就是說,當被觀測物體(手指)與觀測者的距離增加時,由視差產生的位移也成比例地減少。當我們要測量恆星的距離時,首先要計算出一條基線的長度(在上面的實驗中,你雙眼的距離就是作為基線的),這條基線必須足夠長,因為恆星的距離太遠了。如果我們選擇地球一月份的空間位置作為始點,選擇地球七月份時的空間位置作為終點,兩點的距離作為基線才“足夠大”。在一月份和七月份分別觀察被測恆星相對於鄰近背景天體的位置,就得到了恆星的視差值,通常是一個很小的角度。利用基線的長度和這個角度,根據三角關係就可以計算恆星的距離。
貝塞耳選擇了天鵝座中的一顆恆星,並求出半年間該星在天空的角位移移動了約1/5000度。利用這個數據,貝塞耳計算出天鵝座的這顆恆星的距離是94.6萬億千米。雖然當我們參加賽跑比賽,氣喘吁吁地到達終點時,感覺幾千米的賽程真是太遠了;但是在天文學研究中,“千米”作為長度單位實在是太短而不便於使用,就好比用毫米來計算赤道的長度一樣。人們有一把更好的尺子——光年。光年並不是時間單位,而是長度單位,光在一年裡傳播的距離,就是一光年。貝塞耳的數字用光年來表示為10光年多一點。亨德森雖然比貝塞耳較早行動,但由於健康原因,直到貝塞耳發表了結果之後才完成了他的計算。他選擇的恆星是半人馬座α星,因為它在天空中非常明亮,亨德森認為它是因為距離近才如此明亮的。亨德森的判斷是正確的,半人馬座α星距離地球只有4.3光年,是天空中除太陽外離我們最近的恆星。斯特魯維的工作更為艱巨,因為他選擇的研究對象是天琴座中的織女星,距離地球有26光年,由於視差很小,使當年斯特魯維的觀測結果不太準確。
