極角
平面上任何一點到極點的連線和極軸的夾角
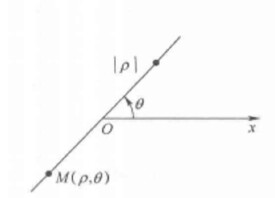
在平面上取一定點O,從O引一條水平射線Ox,規定方向自左至右,再選定一個長度單位並規定角旋轉的正方向,通常取逆時針方向,這樣就構成了一個 極坐標系,如圖1所示,點O叫作 極點,射線Ox叫作極軸。
在極坐標系中,平面上任意一點M的位置,可以由OM的長度和從Ox到OM的角 來確定,把 叫作點M的 極徑,叫作點M的 極角,有序實數對 叫作點M的 極坐標,記作。
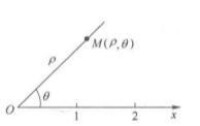
圖1
如圖2所示,在極坐標系中,點 的極坐標分別為。
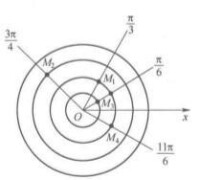
圖2
在實際應用時,極徑 和極角 也可以取負值,當 時,點 在 的終邊上取一點,使,當 時,點 在角 終邊的反向延長線上取一點,使,如圖3所示,當極軸按順時針方向旋轉時, .在如圖4所示的極坐標系中,點 的極坐標分別為。
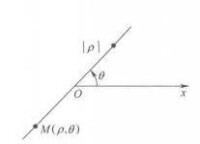
圖3
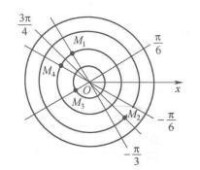
圖4
極坐標系和直角坐標系是兩種不同的坐標系,同一個點既可以用極坐標表示,也可以用直角坐標表示。把直角坐標系的原點作為極點,x軸的正半軸作為極軸,並在兩種坐標系中取相同的長度單位,如圖5所示,設M是平面內任意一點,它的直角坐標是 極坐標是,顯然有
利用上式,可以把點M的極坐標化為直角坐標。
由上面的公式,又可得
利用該公式,可以把點M的直角坐標化為極坐標。
例1 把點M的極坐標 化為直角坐標。
解: 由公式 得
於是得點M的直角坐標為。
例2 把點M的直角坐標 化為極坐標。
解:由公式 得
因為點M在第二象限,所以 於是得點M的極坐標為。