極坐標系

主條目：三角函數的歷史

眾所周知，希臘人最早使用了角度和弧度的概念。天文學家喜帕恰斯（190-120BC）製成了一張求各角所對弦的弦長函數的表格。並且，曾有人引用了他的極坐標系來確定恆星位置。在螺線方面，阿基米德描述了他的著名的螺線，一個半徑隨角度變化的方程。希臘人作出了貢獻，儘管最終並沒有建立整個坐標系統。

關於是誰首次將極坐標系應用為一個正式的坐標系統，流傳著有多種觀點。關於這一問題的較詳盡歷史，哈佛大學教授朱利安·科利奇（Julian Coolidge）的《極坐標系起源》作了闡述。格雷瓜·德·聖-萬桑特和博納文圖拉·卡瓦列里，被認為在幾乎同時、並獨立地各自引入了極坐標系這一概念。聖-萬桑特在1625年的私人文稿中進行了論述並發表於1647年，而卡瓦列里在1635進行了發表，而後又於1653年進行了更正。卡瓦列里首次利用極坐標系來解決一個關於阿基米德螺線內的面積問題。布萊士·帕斯卡隨後使用極坐標系來計算拋物線的長度。

在1671年寫成，1736年出版的《流數術和無窮級數》一書中，艾薩克·牛頓第一個將極坐標系應用於表示平面上的任何一點。牛頓在書中驗證了極坐標和其他九種坐標系的轉換關係。在1691年出版的《博學通報》一書中雅各布·伯努利正式使用定點和從定點引出的一條射線，定點稱為極點，射線稱為極軸。平面內任何一點的坐標都通過該點與定點的距離和與極軸的夾角來表示。伯努利通過極坐標系對曲線的曲率半徑進行了研究。

實際上應用“極坐標”這個術語的是由格雷古廖·豐塔納開始的，並且被18世紀的義大利數學家所使用。該術語是由喬治·皮科克（GeorgePeacock）在1816年翻譯席維斯·拉克魯克斯的《微分學與積分學》一書時，被翻譯為英語的。

亞歷克西斯·克萊羅和萊昂哈德·歐拉被認為是將平面極坐標系擴展到三維空間的數學家。

極坐標

第一個用極坐標來確定平面上點的位置的是牛頓。他的《流數法與無窮級數》，大約於1671年寫成，出版於1736年。此書包括解析幾何的許多應用，例如按方程描出曲線。書中創建之一，是引進新的坐標系。17甚至18世紀的人，一般只用一根坐標軸（x軸），其y值是沿著與x軸成直角或斜角的方向畫出的。

牛頓所引進的坐標之一，是用一個固定點和通過此點的一條直線作標準，例如我們使用的極坐標系。牛頓還引進了雙極坐標，其中每點的位置決定於它到兩個固定點的距離。

由於牛頓的這個工作直到1736年才為人們所發現，而瑞士數學家J.貝努利於1691年在《教師學報》上發表了一篇基本上是關於極坐標的文章，所以通常認為J.貝努利是極坐標的發現者。

J.貝努利的學生J.赫爾曼在1729年不僅正式宣布了極坐標的普遍可用，而且自由地應用極坐標去研究曲線。他還給出了從直角坐標到極坐標的變換公式。確切地講，J.赫爾曼把cosθ,sinθ當作變數來使用，而且用n和m來表示cosθ和sinθ。歐拉擴充了極坐標的使用範圍，而且明確地使用三角函數的記號；歐拉那個時候的極坐標系實際上就是現代的極坐標系。

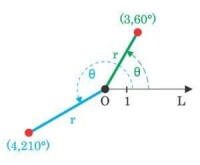
正如所有的二維坐標系，極坐標系也有兩個坐標軸：（半徑坐標）和（角坐標、極角或方位角，有時也表示為或）。坐標表示與極點的距離，坐標表示按逆時針方向坐標距離0°射線（有時也稱作極軸）的角度，極軸就是在平面直角坐標系中的x軸正方向。

比如，極坐標中的（3,60°）表示了一個距離極點3個單位長度、和極軸夾角為60°的點。(−3,240°)和（3,60°）表示了同一點，因為該點的半徑為在夾角射線反向延長線上距離極點3個單位長度的地方（240°−180°=60°）。

極坐標系中一個重要的特性是，平面直角坐標中的任意一點，可以在極坐標系中有無限種表達形式。通常來說，點（r,θ）可以任意表示為（r,θ±n×360°）或（−r,θ±(2n+1)180°），這裡n是任意整數。如果某一點的r坐標為0，那麼無論θ取何值，該點的位置都落在了極點上。

在極坐標系與平面直角坐標系（笛卡爾坐標系）間轉換極

坐標系中的兩個坐標 ρ和 θ可以由下面的公式轉換為 直角坐標系下的坐標值

x=ρcosθ

y=ρsinθ

由上述二公式，可得到從直角坐標系中x和 y兩坐標如何計算出極坐標下的坐標

θ=arctany/x ( x不等於0)

在 x= 0的情況下：若 y為正數 θ= 90° (π/2 radians)；若 y為負，則 θ= 270° (3π/2 radians).

用極坐標系描述的曲線方程稱作極坐標方程，通常表示為r為自變數θ的函數。

極坐標方程經常會表現出不同的對稱形式，如果r(-θ) = r(θ)，則曲線關於極點（0°/180°）對稱，如果r(π-θ) = r(θ)，則曲線關於極點（90°/270°）對稱，如果r(θ-α) = r(θ)，則曲線相當於從極點順時針方向旋轉α°。

方程為r(θ) = 1的圓。

在極坐標系中，圓心在(r0, φ) 半徑為 a 的圓的方程為r^2-2rr0cos(θ-φ)+r0^2=a^2

該方程可簡化為不同的方法，以符合不同的特定情況，比如方程r(θ)=a表示一個以極點為中心半徑為a的圓。

經過極點的射線由如下方程表示θ=φ

,其中φ為射線的傾斜角度，若 k為直角坐標系的射線的斜率，則有φ = arctan k。任何不經過極點的直線都會與某條射線垂直。這些在點（r0, φ）處的直線與射線θ = φ 垂直，其方程為

r(θ)=r0sec(θ-φ)

一條方程為 r(θ) = 2 sin 4θ的玫瑰線。

極坐標的玫瑰線（polar rose）是數學曲線中非常著名的曲線，看上去像花瓣，它只能用極坐標方程來描述，方程如下：

r(θ)=a cos kθ

r(θ)=a sin kθ

OR如果k是整數，當k是奇數時那麼曲線將會是k個花瓣，當k是偶數時曲線將是2k個花瓣。如果k為非整數，將產生圓盤（disc）狀圖形，且花瓣數也為非整數。注意：該方程不可能產生4的倍數加2（如2，6，10……）個花瓣。變數a代表玫瑰線花瓣的長度。

方程 r(θ) = θ for 0 < θ < 6π的一條阿基米德螺線。

阿基米德螺線在極坐標里使用以下方程表示：r(θ)=a+bθ

.改變參數a將改變螺線形狀，b控制螺線間距離，通常其為常量。阿基米德螺線有兩條螺線，一條θ > 0，另一條θ < 0。兩條螺線在極點處平滑地連接。把其中一條翻轉 90°/270°得到其鏡像，就是另一條螺線。

橢圓，展示了半正焦弦

圓錐曲線方程如下：r=ep/(1-e cosθ)

其中l表示半正焦弦，e表示離心率。如果e < 1，曲線為橢圓，如果e = 1，曲線為拋物線，如果e > 1，則表示雙曲線。

其中e表示離心率，p表示焦點到準線的距離。

由於坐標系統是基於圓環的，所以許多有關曲線的方程，極坐標要比直角坐標系（笛卡爾形式）簡單得多。比如lemniscates, en:lima?ons, anden:cardioids。

當限制ρ≥0，0≤θ<2π時，平面上除極點Ο以外，其他每一點都有唯一的一個極坐標。極點的極徑為零，極角任意。若除去上述限制，平面上每一點都有無數多組極坐標，一般地，如果（ρ，θ）是一個點的極坐標，那麼（ρ，θ+2nπ），（－ρ，θ+（2n+1）π），都可作為它的極坐標，這裡n 是任意整數。

平面上有些曲線，採用極坐標時，方程比較簡單。例如以原點為中心，r為半徑的圓的極坐標方程為ρ=r ，等速螺線的極坐標方程為ρ=aθ 。此外，橢圓、雙曲線和拋物線這3種不同的圓錐曲線，可以用一個統一的極坐標方程表示。

對於平面上任意一點p，用ρ表示線段op的長度，稱為點p的極徑或矢徑，從ox到op的角度θ [0，2π]，稱為點p的極角或輻角，有序數對(ρ，θ)稱為點p的極坐標。極點的極徑為零，極角不定。除極點外，點和它的極坐標成一一對應。

（1）用於定位和導航。極坐標通常被用於導航，作為旅行的目的地或方向可以作為從所考慮的物體的距離和角度。例如，飛機使用極坐標的一個略加修改的版本進行導航。這個系統中是一般的用於導航任何種類中的一個系統，在0°射線一般被稱為航向360，並且角度是以順時針方向繼續，而不是逆時針方向，如同在數學系統那樣。航向360對應地磁北極，而航向90，180，和270分別對應於磁東，南，西。因此，一架飛機向正東方向上航行5海里將是在航向90（空中交通管制讀作090）上航行5個單位。

（2）有些幾何軌跡問題如果用極坐標法處理，它的方程比用直角坐標法來得簡單，描圖也較方便。1694年，J.貝努利利用極坐標引進了雙紐線，這曲線在18世紀起了相當大的作用。

（3）建模有徑向對稱的系統提供了極坐標系的自然設置，中心點充當了極點。這種用法的一個典型例子是在適用於徑向對稱的水井時候的地下水流方程。有徑向力的系統也適合使用極坐標系。這些系統包括了服從平方反比定律的引力場，以及有點源的系統，如無線電天線。

（4）行星運動的開普勒定律。開普勒第二定律極坐標提供了一個表達在引力場中開普勒行星運行定律的自然數的方法。開普勒第一定律，認為環繞一顆恆星運行的行星軌道形成了一個橢圓，這個橢圓的一個焦點在質心上。上面所給出的二次曲線部分的等式可用於表達這個橢圓。開普勒第二定律，即等域定律，認為連接行星和它所環繞的恆星的線在等時間間隔所劃出的區域是面積相等的，即d\mathbf{A}\over dt是常量。這些等式可由牛頓運動定律推得。在開普勒行星運動定律中有相關運用極坐標的詳細推導。