復變數
復變數
如果複數是一個變數,則稱為復變數。一個復變數s有一個實部α、一個虛部ω,即s=σ+jω。它可以用s複平面上的一個點來表示。
設 與 為兩任意實數,以 表示 ,則式子 叫做複數。如以兩個實變數 與分別代替 與,則所得式子 就叫做復變數,並記作s(即令 )。若,則,此時復變數變為實變數,所以實變數是復變數的特殊情形。叫做復變數s的實部,記作,叫做復變數s的虛部,記作,即。
復變數(以下簡稱複數) 有以下幾種表示法:
坐標(點)表示法
由於任一複數 與一對實變數 成一一對應關係,所以可以用直角坐標( )表示之。反之,在平面上建立直角坐標系后,每一個點都可以表示為複數。因此,在複數域中 平面又叫做複平面或s平面。軸叫做實軸,軸叫做虛軸。例如圖1所示為s平面,平面上任一點 可由坐標和 來確定。或者記作。
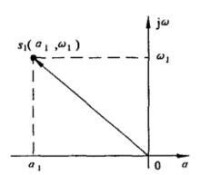
圖1 坐標表示法
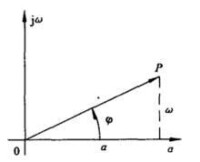
圖2 向量表示法
向量表示法
複數s還可用從原點指向點( )的向量來表示,如圖2所示。向量的長度稱為s的模或絕對值,記作向量 與實軸的夾角 稱為s的輻角,記作。
關於輻角 要注意下列關係:
時,在第一象限; 時,在第二象限;
三角表示法和指數表示法
利用直角坐標與極坐標的關係
複數s可以表示為:這就是複數的三角表示法。
利用歐拉公式: ,可以得到: ,這種形式稱為複數的指數表示法。根據討論問題的需要,可以把複數從一種表示形式轉換為另一種表示形式。
兩個複數乘積的模等於它們的模的乘積;兩個複數乘積的輻角等於它們輻角的和。
根據這個定理,可以說乘積 的向量是從因子 的向量旋轉一個角度 (即 ),並伸長(縮短)到 倍得到的。如圖3所示。特別,當時,乘法變成了只是旋轉。例如 相當於將逆時針旋轉90°,相當於將s順時針旋轉90°。
如果用指數形式表示複數
則乘積定理可以簡明地表示為
兩個複數的商的模等於它們的模的商;兩個複數的商的輻角等於被除數與除數的輻角之差。若 則商定理可以簡明地表示為