特徵線法
特徵線法
method of characteristics 一種基於特徵理論的求解雙曲型偏微分方程組的似方法。它產生較早,19世紀末已經有效地為人們所用。電子計算機出現以後,又得到了進一步的發展,在一維不定常流和二維定常流等問題中得到了廣泛的用。
以偏微分方程的特徵理論為基礎,求解雙曲型偏微分方程的一種近似計算方法。如問題比較簡單,用這種方法可求出分析解或近似的分析解;如問題複雜,也可求得準確度很高的數值解。此外,特徵線法還可用來對雙曲型問題作定性分析,尤其是可用來研究怎樣給出初始條件和邊界條件使問題適定。這對設計求解雙曲型微分方程的其他類型的數值方法有指導意義。特徵線法早在19世紀末就已出現,20世紀30~40年代用手算就已解決不少問題。電子計算機出現后,此方法更趨完善,並得到廣泛應用。

圖1 淺水波的特徵線
(g為重力加速度,h為水的平均厚度),水波便不逆流向上傳播而被水流帶向下游,即石子不影響圖1b中左邊的水流。受某點發出的小擾動影響的區域和不受影響的區域的界線實際上就是特徵線,這種特徵線是肉眼能看見的。在一般情況下,特徵線是肉眼看不見的。例如,表面有條紋的子彈以超聲速穿過空氣,條紋引起的特徵線(圖2)只有藉助儀器才能觀測到。氣體的一維不定常運動可用下述基本方程描述:
式中u為質點速度;ρ為密度;p為壓力;S為熵;x為坐標;t為時間。為求解(1)還要引進聲速c和狀態方程,。式(1)是具有兩個自變數和三個未知函數的雙曲型方程組。它是非線性的。現以解此方程組來說明特徵線法的要點。通過變換可將(1)轉換成等價的方程組(2),(2)的每個方程只包含沿某個方向的微商。這樣的方向就是“特徵方向”。(1)的第三式是沿著方向的微商,因此,就是一個特徵方向。則是相應的沿此方向的特徵關係式。
(1)的第一、二兩個方程經簡單變換后可得:
(2)中兩式分別只有沿方向和dt的微商。因此,就是(1)的另兩個特徵方向。
則是沿這兩個方向的“特徵關係式”。在平面上,由特徵方向所確定的相應的曲線是(1)的特徵線。概括(1)的三個特徵方向和相應的特徵關係式,就得到和(1)等價的常微分方程組:特徵線法正是通過上述的變換,將求解偏微分方程組(1)的問題化成求解簡單得多的常微分方程組(3)的問題。
考慮平面上兩個充分接近的點和(圖3),設這兩點的都已知,把過點的特徵線dt與過點的特徵線dt的交點記作。再從向時間小的方向作特徵線即,u的值暫用,兩點u的平均值。同的交點為。在這些點上,所有各量都用相應的記號表示。為了求點的,然後用狀態方程求出,,可將方程(3)近似地表示為:
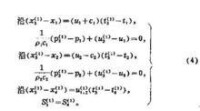
特徵線法
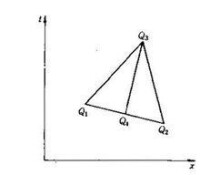
圖3 x-t平面上的特徵線-由Q1,Q2求Q3
(4)中的可以靠和兩點的熵值用內插法求得。從(4)可以求出點的近似位置及其上的值,,。以上的做法只相當於用曲線上一點的切線代替切點附近的曲線,因此數值計算中稱作一級近似(又稱初算)。根據一級近似的結果再算一次(又稱重算),就得到准得多的二級近似解。作法是用Q3點的一級近似值 , , 與點的已知值平均,以代替式(4)中的,。這相當於用割線代替曲線。當然理論上與實際上都更准。同樣用點初算值與點已知值的平均值代替式(4)中的及。當然的位置和也要重新算。這樣得出的,就是用特徵線法求點各量的相當好的數值結果。
如果在一條與特徵線不相切且同t軸方向接近的曲線段MN上給定初值(圖4),則用上法可求出在過M點的特徵線和過N點的特徵線 所圍成的區域MNP內各特徵線交點的近似位置和相應的未知函數值。
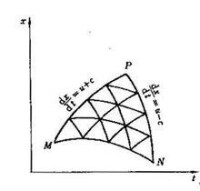
圖4 x-t平面上的特徵線網格
R. Courant and K. O. Friedrichs,Supersonic Flow and Waves,Interscience Pub., London,1956.