共找到2條詞條名為狀態方程的結果 展開
- 流體力學
- 控制科學
狀態方程
流體力學
狀態方程是表徵流體壓強、流體密度、溫度等三個熱力學參量的函數關係式。不同流體模型有不同的狀態方程。它可用下述關係表示p=p(ρT)或U=U(ρT)來表示,式中p為壓強;ρ為流體密度;T為熱力學溫度;U為單位質量流體的內能。完全氣體的狀態方程為p=ρRT,式中R為氣體常數;;R=287. 14m2/(s2K)。比熱為常數的完全氣體的狀態方程為U=CvT,式中Cv為定容比熱。
目錄
物質在平衡狀態下p-V-T關係的數學方程。當壓力足夠低時,各種氣體的p-V-T關係存在簡單的規律。1661年,英國化學和物理學家R.玻意耳根據實驗得出結論:在恆溫下,一定量氣體的體積與壓力成反比。這一規律,后稱玻意耳定律。1802年,法國化學家J.-L.蓋-呂薩克發現:在恆壓下一定量氣體的體積與絕對溫度成正比,后稱蓋-呂薩克定律。1811年,義大利物理學家A.阿伏伽德羅提出:在恆溫恆壓下,同體積任何氣體的摩爾數相同,后稱阿伏伽德羅定律。由這三個定律導出理想氣體狀態方程:
pVm=RT
式中R為摩爾氣體常數,其值為8.3144J/(mol·K);p、T和Vm分別為壓力、絕對溫度和摩爾體積。此式亦可根據對理想氣體的假設(分子間無作用力,分子本身體積可忽略),由氣體分子運動理論導出。
低壓下的實際氣體接近於理想氣體。壓力升高時,實際氣體的p-V-T關係都會偏離理想氣體狀態方程。隨著化肥工業、石油化工等的發展,高壓過程的應用日趨增多,促進了實際氣體狀態方程的研究。這種狀態方程迄今已提出了幾百個,但僅有十多個得到廣泛應用。所有實際氣體狀態方程在壓力趨於零時,都還原為理想氣體狀態方程。狀態方程的研究可用理論方法和半經驗方法,各自得到相應的狀態方程。
理論方程 從分子微觀運動出發,運用統計力學方法導出的狀態方程。例如著名的維里方程(維里一詞來自拉丁文,其意義是力):
就是根據分子間相互作用力的概念,由統計力學導出。式中B、C、D、……依次稱為第二、三、四、……維里係數,分別反映兩分子、三分子、四分子、……間的相互作用,都是溫度的函數。此式適用於密度不太高的氣體。對於更一般的流體,理論方程為:
式中NA為阿伏伽德羅常數;u(r)為分子間相互作用位能函數;r為分子間距;g(r)為徑向分子分佈函數,用以描述流體分子的分佈情況。
近年來理論研究成果顯著。例如:對於相互間沒有吸引力的硬球分子及其混合物,已經導出比較嚴格的硬球狀態方程。但是對於實際流體,由於對它的u(r)、g(r)兩函數的具體形式尚未充分認識,還須借經驗導出適用於實際流體的狀態方程。
半經驗方程 將半經驗模型結合理論方程,或分析已有方程偏離實際情況的原因,引入經驗修正項以改進原有方程,是目前建立半經驗方程所用的主要方法。半經驗方程在工程上應用甚廣,數目也多,並可進一步分為如下兩類:
三次型方程 能展開成為摩爾體積的三次式的半經驗方程。這類方程比較簡單,僅含兩個或三個方程參數。常用的有:
① 范德瓦耳斯方程 J.D.范德瓦耳斯於1873年對理想氣體狀態方程作了修正後,提出的實際氣體狀態方程為:
式中α和b為物質的特徵參數;α/V娽項是分子間的引力對p的校正項;b則是考慮分子本身的體積的校正項。利用臨界點條件,可以由臨界溫度Tc和臨界壓力Hc算出α和b。范德瓦耳斯方程雖然準確度不高,很少用於實際計算,但它的物理意義明確,是其他三次型方程的基礎。
② RK方程 O.雷德利克和J.N.S.鄺於1949年在范德瓦耳斯方程的基礎上提出的一個兩參數方程:
它是形式最簡單的常用狀態方程,一般情況下有一定的準確度。式中α和b亦為物質的特徵參數,由實驗數據回歸求取;但在缺乏實驗數據時,也可由臨界溫度Tc和臨界壓力pc按下式計算而得:
α=0.42748R2T/pc,b=0.08664RTc/pc
RK 方程有不少修正式,其中比較成功的是G.索阿韋於1972年提出的,簡稱為SRK方程,其形式與RK方程相同,只是其中α/T1/2代之以
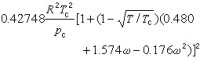
狀態方程
③ PR方程 D.Y.彭和D.B.魯賓遜於1976年提出如下的狀態方程:
式中此方程適用範圍和SRK方程相當,在預測液體飽和體積時,其精度比SRK方程有所提高。
多參數方程 在半經驗方程中,為使求解達到一定的準確度和擴大應用範圍,而建立的一類比三次型方程參數更多的方程。這類方程,由於參數多,所需要的實驗信息和處理數據的工作量都大為增加。應用較廣的多參數方程有:
① BWR方程 M.本尼迪克特、G.B.韋布和L.C.魯賓於1940年提出如下的狀態方程:
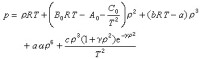
狀態方程
②馬丁-侯方程 J.J.馬丁和侯虞鈞於1955年發表的狀態方程通式如下:
狀態方程
混合物狀態方程 混合物的p-V-T 關係同組成有關。通常將混合物假設為一種純物質,採用一套虛擬特徵參數,就可用與一般純物質相同的狀態方程。虛擬特徵參數是混合物中相應純組分的特徵參數和混合物組成的函數。具體的函數關係則稱混合規則。例如RK方程用於計算二元混合物的p-V-T關係時,採用的混合規則為:
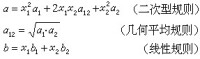
狀態方程
採用理論方程時,原則上不需要混合規則。如一般流體的理論狀態方程推廣到m元混合物,得
式中uij和gij分別為i、j分子對的相互作用位能函數和徑向分佈函數。
研究方向 狀態方程在理論研究和實際應用中都很重要,但迄今為止還沒有一個狀態方程能滿意地應用於所有工程分析,因此有關狀態方程的研究仍很活躍。許多學者正致力於建立普遍適用的、有嚴格理論基礎的狀態方程,目前已取得某些進展,例如對倫納德-瓊斯流體(分子間力遵守倫納德-瓊斯位能函數模型)已建立比較精確的狀態方程。但如考慮到分子的不同形狀,還有大量問題等待解決。因此,關於狀態方程研究的重點仍是半經驗方程。一方面,努力尋找形式簡單、參數較少但又能適用於氣(汽)液兩相以至於臨界區域的新方程,同時擴大現有方程的應用範圍。此外,為更精確地計算混合物的p-V-T關係,正在研究適應範圍廣、精確度高的混合規則。
