費根鮑姆常數
與混沌現象有關的普適常數
費根鮑姆常數是新近發現的、且在學術界認定的一個普適常數,這個常數與“混沌現象”有關。
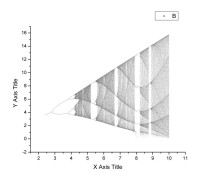
Rossler吸引子的feigenbaum圖
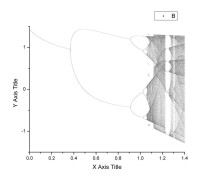
Henon變換的feigenbaum圖
1975年,費根鮑姆用HP-65計算器計算后得出,這種周期倍增分岔(period-doubling bifurcations)發生時的參數之間的差率是一個常數,他為此提供了數學證明。他進一步揭示了同樣的現象、同樣的常數適用於廣泛的數學函數領域,這個普適的結論使數學家們能夠在對錶象不可捉摸的混沌系統的解密道路上邁出了第一步。這個“極限率”(ratio of convergence)現在通稱為費根鮑姆常數。1978年他發表了關於映射的研究的重要論文Quantitative Universality for a Class of Nonlinear Transformations《一個非線性變換類型的量子普適性》,其中特別談到了對於混沌理論有直接意義的Logistic映射。
若αn代表周期2的n次方的分支點(引起分岔時的α臨界值),則(相鄰倍化分岔點間的距離比)是一個常數:
