黃金數分割

在中學數學中講到：將一條線段分成兩部分，使長線段是原線段和短線段的比例中項，叫做把線段黃金分割。分點叫做黃金分割點，長度為1的線段的黃金分割點，大約在距一個端點的0.618處，0.618稱為黃金分割數。黃金分割數與我們的生活有著密切聯繫：

義大利的數學家菲波那契調查了大量的人體數據后得出結論：人從頭頂至臍與臍至腳底之比，臂寬與驅干長度之比，下肢長度與全身長度之比，都約為0.618，只有少數人的這個比值等於0.618，也只有這種人才是“標準的美人”。在人體藝術品中，以這種比例為標準的作品就能獲得最佳藝術效果。莫扎特的“安魂曲”中第一段，第一部分有38次節拍，第二部分有62次節拍，比值約為0.61。

莫扎特正是有意識地把“黃金分割”應用到了自己的音樂作品之中，才能使他的作品演奏起來悅耳動聽、流傳至今。

把一條線段分割為兩部分，使其中一部分與全長之比等於另一部分與這部分之比。其比值是一個無理數，取其前三位數字的近似值是0.618。由於按此比例設計的造型十分美麗，因此稱為黃金分割，也稱為中外比。這是一個十分有趣的數字，我們以0.618來近似，通過簡單的計算就可以發現：

1/0.618=1.618

(1-0.618)/0.618=0.618

這個數值的作用不僅僅體現在諸如繪畫、雕塑、音樂、建築等藝術領域，而且在管理、工程設計等方面也有著不可忽視的作用。

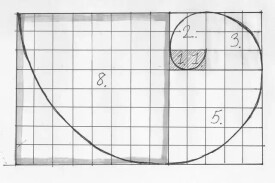
讓我們首先從一個數列開始，它的前面幾個數是：1、1、2、3、5、8、13、21、34、55、89、144…..這個數列的名字叫做"菲波那契數列"，這些數被稱為"菲波那契數"。特點是即除前兩個數（數值為1）之外，每個數都是它前面兩個數之和。

菲波那契數列與黃金分割有什麼關係呢？經研究發現，相鄰兩個菲波那契數的比值是隨序號的增加而逐漸趨於黃金分割比的。即f(n)/f(n-1)-→0.618…。由於菲波那契數都是整數，兩個整數相除之商是有理數，所以只是逐漸逼近黃金分割比這個無理數。但是當我們繼續計算出後面更大的菲波那契數時，就會發現相鄰兩數之比確實是非常接近黃金分割比的。

一個很能說明問題的例子是五角星/正五邊形。五角星是非常美麗的，我們的國旗上就有五顆，還有不少國家的國旗也用五角星，這是為什麼？因為在五角星中可以找到的所有線段之間的長度關係都是符合黃金分割比的。正五邊形對角線連滿后出現的所有三角形，都是黃金分割三角形。

由於五角星的頂角是36度，這樣也可以得出黃金分割的數值為2Sin18。

黃金分割點約等於0．618：1

是指分一線段為兩部分，使得原來線段的長跟較長的那部分的比為黃金分割的點。線段上有兩個這樣的點。

利用線段上的兩黃金分割點，可作出正五角星，正五邊形。

2000多年前，古希臘雅典學派的第三大算學家歐道克薩斯首先提出黃金分割。所謂黃金分割，指的是把長為L的線段分為兩部分，使其中一部分對於全部之比，等於另一部分對於該部分之比。而計算黃金分割最簡單的方法，是計算斐波契數列1，1，2，3，5，8，13，21，...后二數之比2/3,3/5,4/8,8/13,13/21,...近似值的。

黃金分割在文藝復興前後，經過阿拉伯人傳入歐洲，受到了歐洲人的歡迎，他們稱之為"金法"，17世紀歐洲的一位數學家，甚至稱它為"各種演演算法中最可寶貴的演演算法"。這種演演算法在印度稱之為"三率法"或"三數法則"，也就是我們現在常說的比例方法。

其實有關"黃金分割"，我國也有記載。雖然沒有古希臘的早，但它是我國古代數學家獨立創造的，後來傳入了印度。經考證。歐洲的比例演演算法是源於我國而經過印度由阿拉伯傳入歐洲的，而不是直接從古希臘傳入的。

因為它在造型藝術中具有美學價值，在工藝美術和日用品的長寬設計中，採用這一比值能夠引起人們的美感，在實際生活中的應用也非常廣泛，建築物中某些線段的比就科學採用了黃金分割，舞台上的報幕員並不是站在舞台的正中央，而是偏在台上一側，以站在舞台長度的黃金分割點的位置最美觀，聲音傳播的最好。就連植物界也有採用黃金分割的地方，如果從一棵嫩枝的頂端向下看，就會看到葉子是按照黃金分割的規律排列著的。在很多科學實驗中，選取方案常用一種0.618法，即優選法，它可以使我們合理地安排較少的試驗次數找到合理的西方和合適的工藝條件。正因為它在建築、文藝、工農業生產和科學實驗中有著廣泛而重要的應用，所以人們才珍貴地稱它為"黃金分割"。

黃金分割〔Golden Section〕是一種數學上的比例關係。黃金分割具有嚴格的比例性、藝術性、和諧性，蘊藏著豐富的美學價值。應用時一般取1.618，就像圓周率在應用時取3.14一樣。

發現歷史

由於公元前6世紀古希臘的畢達哥拉斯學派研究過正五邊形和正十邊形的作圖，因此現代數學家們推斷當時畢達哥拉斯學派已經觸及甚至掌握了黃金分割。

公元前4世紀，古希臘數學家歐多克索斯第一個系統研究了這一問題，並建立起比例理論。

公元前300年前後歐幾里得撰寫《幾何原本》時吸收了歐多克索斯的研究成果，進一步系統論述了黃金分割，成為最早的有關黃金分割的論著。

中世紀后，黃金分割被披上神秘的外衣，義大利數家帕喬利稱中末比為神聖比例，並專門為此著書立說。德國天文學家開普勒稱黃金分割為神聖分割。

到19世紀黃金分割這一名稱才逐漸通行。黃金分割數有許多有趣的性質，人類對它的實際應用也很廣泛。最著名的例子是優選學中的黃金分割法或0.618法，是由美國數學家基弗於1953年首先提出的，70年代在中國推廣。

|..........a...........|

+-------------+--------+ -

| | |.

| | |.

| B | A | b

| | |.

| | |.

| | |.

+-------------+--------+-

|......b......|..a-b...|

通常用希臘字母表示這個值。

黃金分割奇妙之處，在於其比例與其倒數是一樣的。例如：1.618的倒數是0.618，而1.618:1與1:0.618是一樣的。

確切值為(√5+1)/2

黃金分割數是無理數，前面的1024位為:

1.6180339887、4989484820、4586834365、6381177203、0917980576

2862135448、6227052604、6281890244、9707207204、1893911374

8475408807、5386891752、1266338622、2353693179、3180060766

7263544333、8908659593、9582905638、3226613199、2829026788

0675208766、8925017116、9620703222、1043216269、5486262963

1361443814、9758701220、3408058879、5445474924、6185695364

8644492410、4432077134、4947049565、8467885098、7433944221

2544877066、4780915884、6074998871、2400765217、0575179788

3416625624、9407589069、7040002812、1042762177、1117778053

1531714101、1704666599、1466979873、1761356006、7087480710

1317952368、9427521948、4353056783、0022878569、9782977834

7845878228、9110976250、0302696156、1700250464、3382437764

8610283831、2683303724、2926752631、1653392473、1671112115

8818638513、3162038400、5222165791、2866752946、5490681131

7159934323、5973494985、0904094762、1322298101、7261070596

1164562990、9816290555、2085247903、5240602017、2799747175

3427775927、7862561943、2082750513、1218156285、5122248093

9471234145、1702237358、0577278616、0086883829、5230459264

7878017889、9219902707、7690389532、1968198615、1437803149

9741106926、0886742962、2675756052、3172777520、3536139362

1076738937、6455606060、5922...