時間延緩效應
物理學效應
時間延緩效應又叫做鐘慢效應。
“同時性”具有相對性,那麼時間間隔測量是否隨慣性系的不同而不同,即也具有相對性?現仍以上述火箭車為例對此問題進行討論。
設想在車中(S' 系)一光脈衝從車廂地板上N 點垂直向上發出(事件1),見圖15.4(a),到車廂頂M 點被反射回原地N 點(事件2)。由於在S' 系中,事件1 和 2 發生在同一地點N ,車中的觀測者只要有一隻靜止在此系中的鐘C 即可測得這兩個事件之間間隔,見圖15.4(b)。
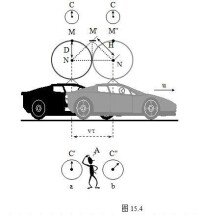
時間延緩效應
(01)
對地面上(S 系)的觀測者A 來說,這兩個事件之間光經歷的路程總長是為2H 的等邊三角形的兩個邊,見圖 15.4(a)、(b),而且由於兩個事件不是發生在同一地點,因此,他必須用放置在事件 1 發生地(與N 點對應)和事件 2 發生地(與N' 點對應)兩隻與C 鍾結構相同並一起校準過的鐘C' 和C" 才能測得這兩個事件之間的時間間隔,設為t ,根據光速不變原理,有
(02)
由三角形NMN',有
(03)
將式 (1)、(2) 代入式 (3) ,消去D 和H ,得
化簡為:
(04)
式中 , ,由於,故,是 0013 表明,在S' 系中測得發生在同一地點的兩個事件之間的時間間隔,在S 系中觀測者看來這兩個事件為異地事件,這兩個事件之間的時間間隔t 總是比 要大,二者之比為。這一現象稱為時間延緩效應。
狹義相對論中,將在一個慣性系中測得的、發生在該慣性系中同一地點的兩個事件之間的時間間隔稱為原時,這裡的t 顯然為原時。時間延緩效應還可表述為:在不同慣性系中測量給定的兩個事件時間間隔,以原時最短。
時間延緩效應還可陳述為,運動時鐘走的速率比靜止時鐘走的速率要慢,實際上,對S 系的觀測來說,靜止在S' 系中的時鐘C 是運動的,他認為運動時鐘C 較他所在慣性系中的時鐘C' 和C" 走的要慢。應當注意,時間延緩效應是相對的,也就是說,對S' 系的觀測者來說,靜止於S 系中的時鐘是運動的,因此相對於自己 系中的鐘走的要慢。
時間延緩效應表明,時間間隔的測量是具有相對性的。
時間延緩效應還表明,事件發生地的空間距離將影響不同慣性繫上的觀測者對時間間隔的測量,也就是說,空間間隔和時間間隔是緊密聯著的。因此,它與時鐘結構無關,是時空本身固有的性質,這也是狹義相對論時空觀與經典時空觀的區別所在。
還應注意,當 時, , ,這時,兩個給定事件間的時間間隔的測量結果對不的關係系相同,即時間間隔測量與參考系無關。這就回到了絕對的時間概念。這表明,絕對時間概念只不過是狹義相對論的時間概念在低速情況下的近似。
時間延緩效應顯著與否決於因子,為了使讀者有一數量級概念,取 ,現將 及的計算值列於表 0001 中。
表 0001 及 的計算值(取 )
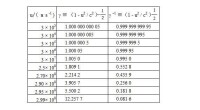
時間延緩效應
雖然如此,有關時間延緩的直接實驗驗證事例還是很多的。
愛因斯坦1879年出生於德國烏爾姆市的一個猶太人家庭(父母均為猶太人),1900年畢業於蘇黎世聯邦理工學院,入瑞士國籍。1905年,獲蘇黎世大學哲學博士學位,愛因斯坦提出光子假設,成功解釋了光電效應,因此獲得1921年諾貝爾物理獎,創立狹義相對論。1915年創立廣義相對論。
為狹義相對論主要思想,擺脫了當時的絕對時間以及絕對靜止的概念。
一般來說,在一個相對我們做高速運動的慣性系中發生的物理過程,在我們看來,他所經歷的時間比在這個慣性系中直接觀察到的時間長。慣性系的速度越大,我們觀察到的過程所經歷的時間也就越長。對於化學反應、生命過程等,這一結論也是正確的。這就是時間延緩效應,又叫做鐘慢效應。
