伽利略變換
伽利略變換
伽利略變換(Galileo transformation)是牛頓力學中所使用的兩個相對做等速直線運動的參考系中的時空變換,屬於一種被動態變換。伽利略變換中,直觀上明顯成立的公式在物體以接近光速運動時就會瓦解,這是相對論性效應造成的。伽利略變換建基於人們加減物體速度的直覺,變換的核心是假設時間、空間是絕對的、彼此獨立的,其中時間均勻流逝,空間均勻分佈且各向同性。
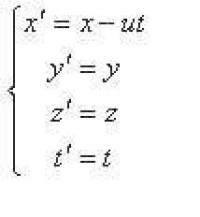
伽利略變換
而時間是均勻流逝的,線性的。
伽利略變換的數學表達式(如右圖)。
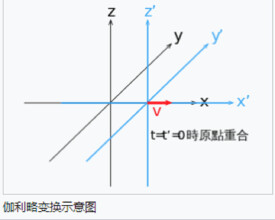
伽利略變換是牛頓力學中所使用的兩個相對做等速直線運動的參考系中的時空變換。設有兩個參考系S(Oxyz)及S'(O'x'y'z'),坐標軸相互平行且軸x與軸x'重合,S'相對S沿x軸以u做等速直線運動,且S系與S'系中各處有結構完全相同的時鐘,記錄的時刻為t與t',並以兩坐標原點O及O'重合時刻為計時起點,則可得某質點m的運動在兩參考系中的時空變換關係:

伽利略
上式即為伽利略(坐標)變換。最後一條方程式意味著時間是不受觀測者的相對運動影響的。
如果將各式對時間求導,則得速度變換式:
vx'=vx-uvy'=vyvz'=vz
因此,如果S是慣性系,即不受外力作用的物體在其中做等速直線運動,則根據上式,它在S'中也一定做等速直線運動,所以S'也是慣性系。如果將各式再一次對時間求導,則得加速度變換關係式:
ax'=axay'=ayaz'=az
亦即a'=a。因此如果S是慣性系,即在其中F=ma成立,則在S'中也有F=ma',所以S'也是慣性系。這樣就從伽利略變換導出了力學相對性原理。
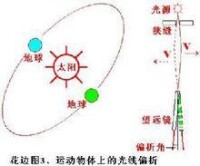
運動物體上的光線也發生了彎曲
間中的一點,t為一維時間中的一點。時空當中的任何一點可以表達為有序對(x,t)。速度為v的均速運動表達為:
(X,t)→(X+tv,t),其中v在R內。
平移表達為:
(X,t)→(X+a,t+b),其中a在內,b在R內。
旋轉表達為:
(X,t)→(GX,t),其中G:R → R為某正交變換。作為一個李群,伽利略變換的維度為10。
伽利略變換與牛頓的絕對時間、絕對空間的概念有關。這裡所謂絕對是指長度的量度與時間的量度均與參考系的運動或參考系的選擇無關。現代物理學中,電、磁、光學現象所符合的相對性原理與伽利略變換髮生了尖銳的矛盾,因此在狹義相對論中修改了絕對時空的概念,空間和時間遵從洛倫茲變換。這時長度與時間的量度都與參考系的速度有關。不過在運動速度遠小於光的速度時,洛倫茲變換近似等於伽利略變換
。