力的合成
力的合成
求兩個或徠兩個以上力的合力,即求與多個分力作用效果相同的一個力的過程或方法叫做力的合成。
力的合成作為物理學學習中必不可少的方法之一,在力學里發揮著至關重要的作用。在掌握力的合成的方法基礎上,可以通過數學計算及推導求出合力的大小及方向,從而在實際生活中對其進行更好的應用。
在大多數實際問題里,物體不只受到一個力,而是同時受到幾個力。如果一個力的作用效果與幾個力共同的作用效果相同,則這一個力就叫做這幾個力的合力。(合力是假想的力,不是真實存在的。)求兩個或兩個以上力的合力的過程或方法叫做力的合成。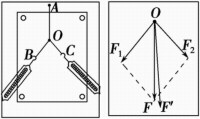

力的合成
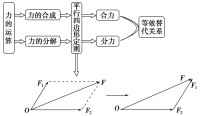
力的合成
匯交力系的合成
各力作用線交於一點的力系稱為匯交力系。根據力的可傳性,作用於剛體的匯交力系可換成各力作用於公共交點的共點力系。利用力的平行四邊形法則(見靜力學公理)將共點力系各力順序合成,就可求得共點力系的合力。合力矢是力多邊形的封閉邊。這種求共點力系的幾何方法稱為力多邊形法。在特殊情況下,若共點力系各力構成的折線的終點和起點重合,即封閉邊為零,則該力系的合力為零,這時力系就成為平衡力系。
平行力系的合成
各力作用線相互平行的一組力稱為平行力系。大小相等而方向相反,作用線不在同一直線上的一對力不能合成為—個力,它們稱為力偶。
任意力系的合成
具有合力的任意力系,其合力的大小和方向還可用合力投影定理(即合力在任一軸線上的投影等於各分力在此軸線上的投影之和)來計算。
同時受幾個力的作用,幾個力如果都作用在物體的同一點,或者它們的作用線相交於同一點,這幾個力叫做共點力。
求兩個或兩個以上力的合力的過程叫做力的合成。
對於非共點力,常見的做法是將各個力移到一個公共作用點上,同時產生相應的彎矩(大小為被移動的力乘以公共點到力作用線的距離),之後再將力和彎矩分別合成。
徠兩個力合成時,以表示這兩個力的有向線段為鄰邊作平行四邊形,這兩個鄰邊之間的對角線就代表合力的大小和方向,這就叫做平行四邊形定則(parallelogramrule)。
兩個矢量合成時,以表示這兩個矢量的有向線段為鄰邊作平行四邊形,這兩個鄰邊之間的對角線就代表合矢量的大小和方向,這就叫做矢量的平行四邊形定則。合矢量的頭對一條分矢量的頭,合矢量的尾對另一條分矢量的尾。
圖中F1與F2夾角為α合力F與F1夾角為 θ
力的合成的平行四邊形定則,只適用於共點力。
如果有兩個以上的共點力作用在物體上,我們也可以應用平行四邊形定則求出它們的合力:先求出任意兩個力的合力,再求出這個合力跟第三個力的合力,直到把所有的力都合進去,最後得到的結果就是這些力的合力。
根據力的平行四邊形則作圖,可以看出,力F1和F2的合力F的大小和方向隨著F1和F2之間的夾角而變化。當夾角等於0度時,力F1和F2在同一直線上且方向相同,F=|F1|+|F2|,合力的大小等於兩個力的大小之和,合力的方向跟兩個力的方向相同。當夾角等於180度時,力F1和F2在同一直線上但方向相反,F=F1-F2,合力的大小等於兩個力的大小之差,合力的方向跟兩個力中較大的那個力的方向相同。
力既有大小,又有方向,力的合成要遵守平行四邊形定則。在物理學中,像這樣的物理量叫做矢量,力是矢量,我們學過的位移,速度,加速度也是矢量。而長度、質量、時間、溫度、能量,路程等物理量,只有大小,沒有方向,在物理學中叫做標量。
其一:先用力F將橡皮筋拉至一定位置,再用兩個不平行的力F1和F2將其拉至同一位置。則3個力的大小可以通過彈簧測力計讀出。在紙上畫出各個力的大小和方向,使其尾段相接,並連接箭頭頂部,則會形成一個四邊形。通過測量各邊的長度並依據平行四邊形的判定法則就可以證明此四邊形為平行四邊形。
其二:設物體A只在F1的作用下在時間t內位移到點B
則AB=0.5at2;=0.5F1/m * t2;
物體A只在F2的作用下在時間t內位移到點C
則AC=0.5 F2/m*t2;
若F1和F2同時存在,則物體A將會位移到D
(四邊行ABCD為平行四邊形)
而物體A若只受F3作用也能在時間t內位移到點D
AD=0.5F/m * t2;
AB:AC:AD=0.5F1/m * t2;:0.5 F2/m*t2;:0.5F3/m * t2;=F1:F2:F3=AS:AQ:AP
在用幾何方法就可以證明四邊形ASPQ為平行四邊形
力的平行四邊形定則以此得證
1.兩分力大小不變時,夾角越大,合力越小
2合力大小的變化範圍 F1+F2 ≥ F ≥ |F1-F2|
3力的合成的平行四邊形定則,只適用於共點力(結論)
