地球繞太陽公轉

橢圓的軌道是地球對附近的天體引力的折中。僅有一個行星和一個恆星的系統是沒有任何意義的。早期的太陽系在形成過程中，原始的行星受到了小行星的撞擊和其他一系列擾動，才導致橢圓軌道的形成。這叫行星徙動理論。

首先：正圓軌道也是橢圓軌道的一種，只不過是特殊的橢圓軌道。

地球繞太陽公轉，在給定的能量的條件下，可能的軌道有無數條，圓軌道只是其中的一條而已。如果想要地球按正圓軌道運行，地球的能量，動量要滿足一定條件。就是任一時刻，地球的動能Ek和勢能Ep的關係滿足 Ek = -Ep/2。或者說當 Ek = -Ep/2時，地球運動方向垂直於日地連線。這個條件非常苛刻，即便是地球在正圓軌道上運行，一點微小的擾動都可以改變這種狀態，使得地球在新的橢圓軌道上運行。

平均角速度是每年360度，即每日59分。平均線速度為每年940，000，000公里，即每秒29.78公里。即時角速度和即時線速度有季節變化，在能量守恆的前提下，離太陽越近，位能越小，動能則越大，即時線速度和即時角速度就越大。在角動量守恆的前提下，即在相等長度的時間內，地球、太陽連線所掃過的面積是恆定的。

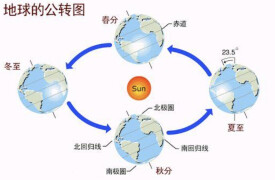
地球的自轉軸與其公轉的軌道面成66°34′的傾斜。這個角度同人們拿鉛筆書寫時筆桿與桌面的傾斜相仿。人們有時形象地比喻為地球“斜著身體”繞太陽公轉。

地球的自轉同它公轉之間的這種關係，天文學和地理學上通常用它的餘角（23°26′），即赤道面與軌道面的交角來表示；而在地心天球上，則表現為黃道與天赤道的交角，並被稱為黃赤交角，又稱"黃赤大距"。黃道與天赤道的兩個交點，叫白羊宮（白羊座）第一點和天秤宮（天秤座）第一點，在北半球分別稱為春分點和秋分點，合稱二分點。黃道上距天赤道最遠的兩點，叫巨蟹宮（巨蟹座）第一點和摩羯宮（摩羯座）第一點，即北半球的夏至點和冬至點，合稱二至點。二至點距天赤道23°26′，稱黃赤大距，是黃角交角在地心天球上的表現。

黃赤交角在天球上也表現為南北天極對於南北黃極的偏離。天軸垂直於赤道面，黃軸垂直於黃道面，既然黃赤交角是23°26′，那麼，天極對於黃極的偏離，必然也是23°26′

黃赤交角的存在，具有重要的天文和地理意義。前已述及，黃赤交角是地軸進動的成因之一；它還是視太陽日長度周年變化的主要原因。下節還將要說明，黃赤交角是地球上四季變化和五帶區分的根本原因。

開普勒的行星運動定律，讓17世紀初天文學家眼中的太陽系與其真實面貌達到了空前的一致。太陽位於中心；當時已知的六顆行星——水星、金星、地球、火星、木星還有土星由內到外依次在各自的橢圓軌道上圍繞著太陽運動。然而這幅太陽系的“全家福”之中還有一個重大的缺憾，它是沒有比例尺的，因為當時的天文學家不知道任何一顆行星到太陽的距離，他們所知道的只是這些行星與太陽之間的距離的比值，其中地球與太陽之間的平均距離被定為一個天文單位，以此類推最內側的水星與太陽的距離便為0.3871個天文單位，而最外側的土星則在距離太陽9.5388的軌道上緩慢運行。

由於“天文單位”是天文學，特別是天文測量學中一個非常重要的一個天文數值，因此準確的測量地球與太陽之間的距離便成為了“最為崇高的天文問題”之一。

但是這並不是一件容易的事情，太陽高高地掛在空中、遙不可及，顯然不能像測量你家房間大小那樣直接用皮尺去量，而只能通過間接的方法去測定。天文學家們很快便想到了“視差”，所謂的“視差”是指在兩個不同的點上觀察同一個目標時所產生的方向差異，這種方向差異可以通過目標在遙遠背景上的移動計算出來，如果兩點之間的距離是已知的，利用中學所學的幾何學知識就能夠計算出目標到觀測點的距離。我們很容易想到，目標的距離越遠，它的視差就越小，當物體的距離非常遙遠的時候，它的視差便可以忽略不計了，而被當作觀測的背景。日常生活中最為常見的視差，便是當你分別用左右眼看同一個物體時，它在你的眼中相對於其他物體所發生的移動。

但是要測定太陽的視差卻同樣也是一件非常困難的事。首先它的距離太遠，即使分別在地球的兩端來測量，它的視差還是很小，這就需要非常精密的儀器；更為糟糕的是太陽實在是太亮了，它把可以作為背景的星空完全淹沒了，因此我們也就沒有了標尺，這使得直接測量它的視差幾乎成為了一件不可能完成的任務。這幅沒有比例尺的太陽系地圖也就一直使用到了18世紀初。

1716年，英國著名的天文學家、哈雷彗星的發現者，埃德蒙多·哈雷提出了一種間接測定太陽視差的方法，這種方法需要利用一種罕見的天文現象——“金星凌日”，也就是金星製造的微小“日食”，當這種現象發生的時候，在地球上可以看到有一個小黑點兒，也就是金星的影子，從太陽表面經過。哈雷的方法就是通過測定不同觀測地點，這個小黑點經過太陽表面的時間，然後再經過一系列計算，就可以得到太陽的視差。

但是很遺憾的是哈雷沒有等到下次金星凌日的出現便去世了。德國天文學機恩克利用1761年和1769年的兩次金星凌日時的觀測結果，於1824年計算出了太陽與地球之間的距離為1.53億公里。後來的天文學家又利用隨後兩次發生在1874和1882年的金星凌日現象，把這個數字精確到了1.4934億±9.6萬公里，這已經非常接近現代的數值1.49597870億公里。

當然這個數值是太陽與地球之間的平均距離，也就是幾何學中橢圓的半長軸。不過地球軌道非常接近正圓，它目前的偏心率只有0.0174，也就是它與太陽之間最遠的距離只比這個平均距離遠1.74%，大約是260萬公里。

365天6小時9分9.5秒

24小時36分38秒

366天 閏年

36分38秒

整百的年份 要能被400整除才算閏年

恆星年是太陽在天球上連續兩次通過某一恆星所需的時間，長度為365.25636平太陽日。

回歸年是太陽在天球上連續兩次通過春分點所需的時間，長度為365.24220平太陽日。

地球公轉軌道和方向 地球在公轉過程中，所經過的路線上的每一點，都在同一個平面上，而且構成一個封閉曲線。這種地球在公轉過程中所走的封閉曲線，叫做地球軌道。如果我們把地球看成為一個質點的話，那麼地球軌道實際上是指地心的公轉軌道。嚴格地說，地球公轉的中位位置不是太陽中心，而是地球和太陽的公共質量中心，不僅地球在繞該公共質量中心在轉動，而且太陽也在繞該點在轉動。但是，太陽是太陽系的中心天體，地球只不過是太陽系中一顆普通的行星。太陽的質量是地球質量的33萬倍，日地的公共質量中心離太陽中心僅450千米。這個距離與約為70萬千米的太陽半徑相比，實在是微不足道的，與日地1.5億千米的距離相比，就更小了。所以把地球公轉看成是地球繞太陽（中心）的運動，與實際情況是十分接近的。地球軌道的形狀是一個接近正圓的橢圓，太陽位於橢圓的一個焦點上。橢圓有半長軸、半短軸和半焦距等要素，分別用a、b、c表示，其中a又是短軸兩端對於焦點（F1、F2）的距離。半焦距與半長軸和平短軸之間存在著這樣的關係：即 c2=a2-b2 半焦距c與半長軸a的比值c/a，是橢圓的偏心率，用e表示，即e=c/a，偏心率是橢圓形狀的一種定量表示，e的數值大於0而小於1。橢圓越接近於圓形，則e的數值就越小，即接近於0；反之，橢圓越扁，e的數值就越大。經過測定，地球軌道的半長軸a為14960萬千米，半短軸b為14958萬千米。根據這個數據計算出地球軌道的偏心率為：可見，地球軌道非常接近於圓形。由於地球軌道是橢圓形的，隨著地球的繞日公轉，日地之間的距離就不斷變化。地球軌道上距太陽最近的一點，即橢圓軌道的長軸距太陽較近的一端，稱為近日點。在近代，地球過近日點的日期大約在每年一月初。此時地球距太陽約為14710萬千米，通常稱為近日距。地球軌道上距太陽最遠的一點，即橢圓軌道的長軸距太陽較遠的一端，稱為遠日點。在近代，地球過遠日點的日期大約在每年的7月初。此時地球距太陽約為15210萬千米，通常稱為遠日距。近日距和遠日距二者的平均值為14960萬千米，這就是日地平均距離，即1個天文單位。根據橢圓周長的計算公式： L=2πα（1-0.25×e2）計算出地球軌道的全長是94000萬千米。