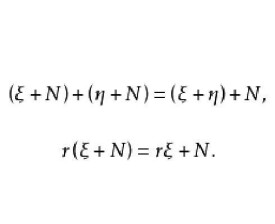商模
商模
商模(quotient module)是模論的重要概念之一，模M與它的商模M-之間的性質有著密切的聯繫。它是將A模M的元素進行陪集分類后所得到的新模，亦稱“差模”。設是上左模的一個子模，則商群M/N中可定義R中元素的作用：a(x+N)=ax+N，其中a∈R，x∈M，x+N∈M/N，則M/N成為一個模，稱為M關於N的商模，同樣可定義右模的商模。
設M是一個R-模，N是M的一個R-子模，則N是加法群M的子群，於是有商群M/N，它的元素是N在M內的陪集，因為N為R-子模，我們可以把M/N作成R-模，在商群內有加法：
對於，我們規定
因為當 時， ．而N是R-子模，所以，這就說明。
在商群M/N上按上面方法定義的R-模稱為模M關於子模N的 商模，仍使用符號M/N表示這個商模。
定理1 設B是R-模，D是B的子模，另有 也是B的子模，且滿足，則商模與 之間滿足。反之，若已知M是的子模，則一定存在B的子模，滿足 且有。
令A，B是R的兩邊理想，置
即AB是由所有的乘積ab生成的加群，易見AB是一個理想，叫作 理想A與B之積。
註：
令C是R的兩邊理想，則：
(1)說C是R的 強素理想： 。
(2)說C是R的 素理想： 。
(3)r稱為 左零因子： 。
類似地，可定義 右零因子。
(4)說R中沒有零因子：中不存在左右零因子。
(5)令，叫作 右逆或 左逆，或者叫r的 逆元素： ,或者，或者。
註：
(1)如果存在右零因子，則一定存在左零因子，反之亦然。
(2)如果 分別是r的左、右逆元：則。
由定義1易知：
(1)C是強素理想 是R的素理想。
(2)如果R是交換的，則(1)之逆也成立。
令C是R的兩邊理想，則下述命題成立：
(1)C是R的強素理想 沒有零因子。
(2)C是R的素理想 零理想是的素理想。
(3)C是R的兩邊理想是單的。
(4)C是R的極大右理想 是體。
基本信息
- 外文名
- quotient module