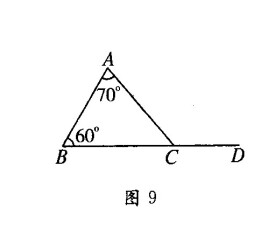
三角形的外角

三角形的外角三角形的一邊與另邊的反向延長線組成的角。

三角形三個外角之和為360° 。三角形的每個頂點處都有兩個相等的外角，所以每個三角形都有六個外角。

三角形的一個外角大於與它不相鄰的任一內角，且三角形的一個外角等於不相鄰的兩個內角和。

三角形一個內角的一邊與另一邊的反向延長線所夾的角。亦即“三角形內角的鄰補角”。三角形的每個頂點處都有兩個相等的外角，所以每個三角形都有六個外角。

三角形的一個外角等於與它不相鄰的兩個內角的和。.

三角形的一個外角大於與它不相鄰的任一內角.

定理：三角形的一個外角等於不相鄰的兩個內角和。

定理：三角形的三個內角和為180度。（三角形內角和定理）定理：多邊形的外角和都等於360度。拓展：在三角形中，已知其中兩個角的度數，根據三角形內角和定理，則能求出第三個角的度數。

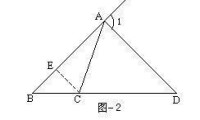
三角形的外角

三角形的外角平分線定理：三角形的外角平分線外分對邊所成的兩條線段和相鄰兩邊對應成比例。

例。已知如圖.△ABC中，∠BAC的外角平分線交BC的延長線於點 D，求證：

證明：過C作AD的平行線交AB於點E。

證明2:

(h為BD邊上的高)

得變形得

性質：三角形的外角和等於360°。

已知∠BAF,∠CBD,∠ECA是△ABC的三個外角，求證

證法1：如圖22.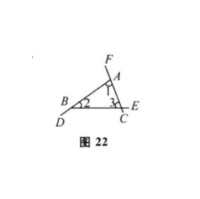

三角形的外角

證法2：如圖23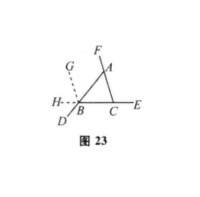

三角形的外角

作CB的延長線BH,過點B作BG∥CA

（1）多邊形外角的定義：多邊形內角的一邊與另一邊的反向延長線所組成的角叫做這個多邊形的外角。在每一個頂點處取這個多邊形的一個外角，它們的和叫做這個多邊形的外角和。

（2）多邊形外角和定理：多邊形的外角和都等於360°。