超限遞歸定理
超限遞歸定理
超限遞歸定理(transfinite recursive theorem)是遞歸定理的推廣,該定理斷言:對任意函數F:V→V,存在惟一的函數G:ord→V,使得對任意α∈ord有G(α)=F(G|α),這裡V表示一切集合構成的類,G|α表示函數G在α上的限制。當在上述定理限於考慮函數G:ω→V這一特殊情形時,定理就變成平常的遞歸定理。超限遞歸定理是馮·諾伊曼(J.von Neumann)於1923年提出的,該定理的意義是,由已給的函數F,以集合G(β)|β<α為F的自變數,所確定的函數值作為被定義函數G在α上的值,所定義出的函數G是惟一確定的,這種定義函數的方法不同於一般的定義方法,因為在定義G(α)時要用到已給的F,而且要用到各個G(β),β<α 。
超限遞歸定理 對於每一個公式γ(x,y)有下述定理:設(A,<)為良序集,且對任何f有唯一的y使γ(f,y)成立,則存在唯一以A為定義域的函數F,使得對於A中的所有t,有:
γ(F↾Seg t,F(t)),
其中 Seg t={x|x
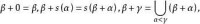 即用關於α的超限歸納原理來定義β+α。同樣地可以定義序數的積和冪,以及相應的運算性質,如結合律等。
即用關於α的超限歸納原理來定義β+α。同樣地可以定義序數的積和冪,以及相應的運算性質,如結合律等。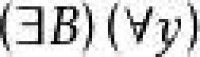
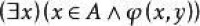
這是個定理模式,表明有無限多個定理,對於每一個γ(x,y),它都是一個定理。
有了良序集,便可在其上建立兩個重要的定理,即超限歸納定理和超限遞歸定理,它們是研究超限無窮集合的主要基礎。所謂超限無窮集合是指超過自然數集合ω的任何無窮集合,由於ω是第一非有限的、最小的無窮集合,是第一個遇到的極限序數,超過這個極限序數的無窮集合論證問題都屬於超限問題,歸納定理的主要功能是克服了無窮元都要論證的困難。而遞歸定理的主要功能是確立運算函數的存在,給出計數的特性,以及其它論證中的作用。
在定義序數運算(加、乘、冪)時,需要用超限遞歸定理:若G是一運算,則有一運算F,使得對每一序數α,都有F(α)=G(F↾α)。而這一定理的證明要用到代換公理。有了代換公理還可以得到極限序數ω+ω的存在性。如果先將正整數從小排到大,再把非正整數從大排到小而成一序列:1,2,3,…,0,-1,-2,…。從而全體整數就良序了,其序型即為ω+ω 。
事實上,任一良序集<ω,<>,都有唯一的序數α使得<ω,<>序同構於<α,∈>。因此,就可以把良序集按序同構來分類,並將同屬於一類的稱為具有同一序型的良序集。而序數就可定義作為同構的良序集的代表。依此,可以定義序數的運算。例如,序數的加法可以定義如下:若α,β為序數,γ為極限序數。
超限遞歸定理
超限遞歸定理的證明需要應用下面的代換公理。
代換公理對於任何集合A和一個具有函數性質且不含B的公式φ(x,y)有:
超限遞歸定理
超限遞歸定理
(y∈B⇆),
或完全形式地表示為:
(∀A)((∀x)(∃!y)(x∈A^φ(x,y)→(∃B)(∀y)(y∈B⇆(∃x)(x∈∧φ(x,y))))。
如果把φ(x,y)理解為“x被代換成y”,代換公理可表述成:若A的每個元至多被代換一個對象,則所有被代換的對象就構成了一個集合B 。
目錄