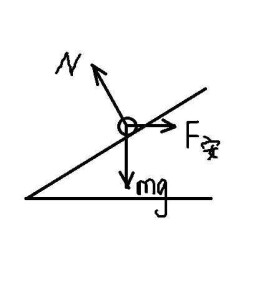
三力平衡
物體受三個力作用處於平衡狀態
而這三個力可能互成角度,也可能在一條直線上·
對於三力平衡,一般根據“任意兩個力的合力與第三個力等大反向”的關係,藉助三角函數、相似三角形等手段求解;或將某一個力分解到另外兩個力的反方向上,得到的這兩個分力勢必與另外兩個力等大、反向;對於多個力的平衡,利用先分解再合成的正交分解法。
物體在三個力的作用下處於平衡狀態,要求我們分析三力之間的相互關係的問題叫三力平衡問題,這是物體受力平衡中最重要、最典型也最基礎的平衡問題。這種類型的問題有以下幾種常見題型。
① 三個力中,有兩個力互相垂直,第三個力角度(方向)已知。
② 三個力互相不垂直,但夾角(方向)已知《考試說明》中規定力的合成與分解的計算只限於兩力之間能構成直角的情形。三個力互相不垂直時,無論是用合成法還是分解法,三力組成的三角形都不是直角三角形,造成求解困難。因而這種類型問題的解題障礙就在於怎樣確定研究方法上。解決的辦法是採用正交分解法,將三個不同方向的力分解到兩個互相垂直的方向上,再利用平衡條件求解。
③ 三個力互相不垂直,且夾角(方向)未知
三力方向未知時,無論是用合成法還是分解法,都找不到合力與分力之間的定量聯繫,因而單從受力分析圖去求解這類問題是很難找到答案的。要求解這類問題,必須變換數學分析的角度,從我們熟悉的三角函數法變換到空間幾何關係上去考慮,因而這種問題的障礙點是如何正確選取數學分析的方法。
解決這種類型的問題的對策是:首先利用合成法或分解法作出三力之間的平行四邊形關係和三角形關係,再根據力的三角形尋找與之相似的空間三角形,利用三角形的相似比求解。
④ 三力的動態平衡問題
即三個力中,有一個力為恆力,另一個力方向不變,大小可變,第三個力大小方向均可變,分析第三個力的方向變化引起的物體受力的動態變化問題。
圖例:老式桿秤
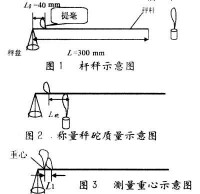
三力平衡
這種類型的問題不需要通過具體的運算來得出結論,因而障礙常出現在受力分析和畫受力分析圖上。在分析這類問題時,要注意物體“變中有不變”的平衡特點,在變中尋找不變數。即將兩個發生變化的力進行合成,利用它們的合力為恆力的特點進行分析。在解決這類問題時,正確畫出物體在不同狀態時的受力圖和平行四邊形關係尤為重要。