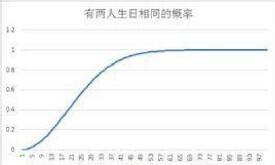
生日悖論
用於檢測哈希函數的理論
從引起邏輯矛盾的角度來說生日悖論並不是一種悖論，從這個數學事實與一般直覺相抵觸的意義上，它才稱得上是一個悖論。大多數人會認為，23人中有2人生日相同的概率應該遠遠小於50%。計算與此相關的概率被稱為生日問題，在這個問題之後的數學理論已被用於設計著名的密碼攻擊方法：生日攻擊。
著名的生日悖論
23個人里有兩個生日相同的人的幾率有多大呢？
居然有50%
問題是這樣的：如果一個房間里有23個或23個以上的人，那麼至少有兩個人的生日相同的概率要大於50%。這就意味著在一個典型的標準小學班級(30人)中，存在兩人生日相同的可能性更高。對於60或者更多的人，這種概率要大於99%。
不計特殊的年月，如閏二月。
先計算房間里所有人的生日都不相同的概率，那麼
第一個人的生日是 365選365
第二個人的生日是 365選364
第三個人的生日是 365選363
:
:
:
第n個人的生日是 選
所以所有人生日都不相同的概率是：
那麼，n個人中有至少兩個人生日相同的概率就是：
所以當的時候，概率為0.507
當的時候，概率為0.999999692751072
對於已經確定的個人，生日不同的概率會發生變化。下面用 隨機變數計算：
令X[i,j]表示第i個人和第j個人生日不同的概率，則易知任意X[i,j]=364/365
令事件A表示n個人的生日都不相同
P(A)=
解，由對數可得：
相比之下，隨機變數也同樣的簡單易懂，且計算起來要方便得多
理解生日悖論的關鍵在於領會相同生日的搭配可以是相當多的。如在前面所提到的例子，23個人可以產生種不同的搭配，而這每一種搭配都有成功相等的可能。從這樣的角度看，在253種搭配中產生一對成功的配對也並不是那樣的不可思議。
換一個角度，如果你進入了一個有著22個人的房間，房間里的人中會和你有相同生日的概率便不是50%了，而是變得非常低。原因是這時候只能產生22種不同的搭配。生日問題實際上是在問任何23個人中會有兩人生日相同的概率是多少。
生日悖論普遍的應用於檢測哈希函數:N-位長度的哈希表可能發生碰撞測試次數不是次而是只有次。這一結論被應用到破解cryptographic hash function的生日攻擊中。
生日問題所隱含的理論已經在[Schnabel 1938]名字叫做capture-recapture的統計試驗得到應用，來估計湖裡魚的數量。
悖論是指一種導致矛盾的命題。悖論(paradox)來自希臘語“para+dokein”，意思是“多想一想”。如果承認它是真的，經過一系列正確的推理，卻又得出它是假的；如果承認它是假的，經過一系列正確的推理，卻又得出它是真的。
把集合分成兩類，凡是不以自身作為元素的集合稱為正常集，（例如，自然數集N本身不是一個自然數，因此N是正常集。）凡是以自身作為元素的集合稱為異常集。（例如，所有的非生物的集合F也是非生物，因此F是異常集。）
這樣，許多日常中常見的悖論(說謊者悖論，理髮師悖論，上帝悖論等)都可以歸入異常集之中了。
另外一種悖論是關於無限的，雖然我們基本上都能接受極限的理論，但是要把這個理論向那些不懂的人解釋還是十分困難的。
(古希臘數學家芝諾（Zeno of Elea）的阿基里斯悖論)阿基里斯在賽跑中不可能追上起步稍微領先於他的烏龜，因為當他要到達烏龜出發的那一點，烏龜又向前爬動了。阿基里斯和烏龜的距離可以無限地縮小，但永遠追不上烏龜。
(古希臘數學家芝諾（Zeno of Elea）的二分法悖論)當一個物體行進一段距離到達D，它必須首先到達距離D的二分之一，然後是四分之一、八分之一、十六分之一、以至可以無窮地劃分下去。因此，這個物體永遠也到達不了D。
“1厘米線段內的點與太平洋麵上的點一樣多”
康托爾（1845－1918）成功地證明了：一條直線上的點能夠和一個平面上的點一一對應，也能和空間中的點一一對應。由於無限，1厘米長的線段內的點，與太平洋麵上的點，以及整個地球內部的點都“一樣多”。
基本信息
- 中文名
- 生日悖論
- 外文名
- birthday paradox
- 運用領域
- 密碼學、哈希表
- 拼音
- shēng rì bèi lùn
- 類型
- 數學名詞
- 性質
- 科學
- 屬於
- 概率論