極限誤差

“極限誤差”術獻釋：

、謂極限誤差指技術標準、檢程計量器具規允誤差值。謂商品計量負偏差指商品量際值低商品算標稱量狀況。

、達形式：測量誤差限誤差限(稱極限誤差，曾極限誤差詞義非)。

3、但是使用中將s與σ不分的現象相當普遍，s當作σ運用，並把它的三倍稱為極限誤差，認為真值存在於±3σ之內的或然率為99.73%，這是錯誤的。

4、對於某一項調查來說，根據客觀要求一般應有一個允許的誤差限，若抽樣誤差在這個限度之內就認為是可允許的，這一允許的誤差限度就稱為極限誤差。根據理論上的要求，抽樣極限誤差通常需要以抽樣平均誤差為根據。

什麼是抽樣極限誤差

抽樣極限誤差又稱“置信區間和抽樣允許誤差範圍”，是指在一定的把握程度（P）下保證樣本指標與總體指標之間的抽樣誤差不超過某一給定的最大可能範圍，記作Δ。

抽樣極限誤差的計算

作為樣本的隨機變數——抽樣指標值（或p），是圍繞以未知的僅能確定的全及指標真值（或P）為中心上下波動，它與全及指標值可能會產生正或負離差，這些離差均是抽樣指標的隨機變數，因而難以避免，只能將其控制在預先要求的誤差範圍（或）內。

或由於和是預先給定的抽樣方案中所允許的誤差範圍，所以利用和可以反過來估計未知的全及指標的取值可能的範圍。解上述兩個絕對值不等式便可得：

例1：例如要估計北京北站整車到達貨物的平均運送時間。從交付的全部整車貨票共26193批中，用不重複抽樣抽取2718批貨票。若允許的抽樣極限誤差（天），經計算知所抽取的每批貨物平均運送時間為（（天），那麼北京北站整車到達貨物的平均運送時間區間估計為（5.64-0.125，5.64+0.125），即在5.515到5.765天之間。

例2：資料同上，若要估計北京北站整車到達貨物的逾期運到率（報告期內超過規定貨物運到期限運到的貨物批數/貨物的到達總批數），從隨機抽取的2718批貨票中，計算得抽樣逾期到率為6.43%，所確定的抽樣極限誤差為，由此可得北京北站總體的逾期運到率的區間估計是（6.43%-0.642%,6.43%+0.642%）。

沖件的極限誤差是具有極限偏差的沖件所具有的實際允許的最大尺寸誤差。這類沖件通常是在沖模失效報廢前沖制的最後一批合格沖件。

對各類沖模沖件誤差在沖模整個壽命中出現的波動、增減趨向及規律等進行全面分析便可發現：沖件誤差的主導部分是不變的；因刃口或型腔的自然磨損而出現的誤差增量隨沖模刃磨沖數增加而使這部分誤差逐漸加大；還有部分誤差的增量是非常規的、不可預見的。所以，各類沖模沖件誤差是由因定誤差、漸增誤差、系統誤差及偶發誤差等幾部分綜合構成。

固定誤差：新沖模在指定的衝壓設備上投入使用至失效報廢的整個(總)壽命過程中，其合格沖件誤差的主導部分固定不變即所謂固定誤差。其大小就是新沖模第一次刃磨前沖制的合格沖件的偏差，也即沖模的初始誤差，而此時的沖模具有初始衝壓精度。刃磨后的沖模，因其工作零件(凸、凹模)磨損而改變尺寸誤差，使沖件識差增量隨刃磨次數增加而逐漸加大，故沖模刃磨后的衝壓精度亦稱“刃磨精度”比其初始精度要低。沖模沖件的固定誤差取決於以下各要素：沖件的材料種類、結構(形狀)尺寸及料厚。

沖裁間隙的大小及其均勻度對沖裁件的尺寸精度有決定性的影響。不同沖裁工藝、不同材料種類與不等料厚，間隙相差懸殊，衝壓精度差異很大。同一種模數m=0.34的2mm的料厚、中心有孔的H62黃銅材料片齒輪複合模沖件，當取間隙C=0.5%t(單邊)，用複合精沖模沖制，沖件尺寸精度達到IT7級，沖件平直無拱彎，沖切面垂直度可達89.5°，其表面粗糙Ra值為0.2μm；而用普通複合模沖制，間隙C=5%t(單邊)，沖件初始誤差亦即沖模的初始衝壓精度為1T9級，沖切面粗糙度Ra值為12.5μm，毛刺高度為0.10mm；還是這個沖件用連續模沖制，間隙C=7%t(單邊)，初始沖件精度為IT11級，沖切面更粗糙，甚至有肉眼可見的台階。通常情況下，沖件材料及其厚度t是選取沖裁間隙的主要依據。一旦選定間隙就確定了沖件的平面尺寸的固定誤差的主體；沖件結構剛度及立體形狀則影響其形位精度。

測量不確定度和誤差是計量學中研究的基本命題，也是計量測試人員經常運用的重要概念之一。它直接關係著測量結果的可靠程度和量值傳遞的準確一致。然而很多人由於概念不清，很容易將二者混淆或誤用，本文結合學習《測量不確定度評定與表示》的體會，著重談談二者之間的不同之處。

首先要明確的是測量不確定度與誤差二者之間概念上的差異。

測量不確定度表徵被測量的真值所處量值範圍的評定。它按某一置信概率給出真值可能落入的區間。它可以是標準差或其倍數，或是說明了置信水準的區間的半寬。它不是具體的真誤差，它只是以參數形式定量表示了無法修正的那部分誤差範圍。它來源於偶然效應和系統效應的不完善修正，是用於表徵合理賦予的被測量值的分散性參數。不確定度按其獲得方法分為A、B兩類評定分量。A類評定分量是通過觀測列統計分析作出的不確定度評定，B類評定分量是依據經驗或其他信息進行估計，並假定存在近似的“標準偏差”所表徵的不確定度分量。

誤差多數情況下是指測量誤差，它的傳統定義是測量結果與被測量真值之差。通常可分為兩類：系統誤差和偶然誤差。誤差是客觀存在的，它應該是一個確定的值，但由於在絕大多數情況下，真值是不知道的，所以真誤差也無法準確知道。我們只是在特定的條件下尋求最佳的真值近似值，並稱之為約定真值。

通過對概念的理解，我們可以看出測量不確定度與測量誤差的主要有以下幾方面區別：

一。評定目的的區別：

測量不確定度為的是表明被測量值的分散性；

測量誤差為的是表明測量結果偏離真值的程度。

二。評定結果的區別：

測量不確定度是無符號的參數，用標準差或標準差的倍數或置信區間的半寬表示，由人們根據實驗、資料、經驗等信息進行評定，可以通過A，B兩類評定方法定量確定；

測量誤差為有正號或負號的量值，其值為測量結果減去被測量的真值，由於真值未知，往往不能準確得到，當用約定真值代替真值時，只可得到其估計值。

三。影響因素的區別：

測量不確定度由人們經過分析和評定得到，因而與人們對被測量、影響量及測量過程的認識有關；

測量誤差是客觀存在的，不受外界因素的影響，不以人的認識程度而改變；

因此，在進行不確定度分析時，應充分考慮各種影響因素，並對不確定度的評定加以驗證。否則由於分析估計不足，可能在測量結果非常接近真值(即誤差很小)的情況下評定得到的不確定度卻較大，也可能在測量誤差實際上較大的情況下，給出的不確定度卻偏小。

四。按性質區分上的區別：

測量不確定度不確定度分量評定時一般不必區分其性質，若需要區分時應表述為：“由隨機效應引入的不確定度分量”和“由系統效應引入的不確定度分量”；

測量誤差按性質可分為隨機誤差和系統誤差兩類，按定義隨機誤差和系統誤差都是無窮多次測量情況下的理想概念。

五。對測量結果修正的區別：

“不確定度”一詞本身隱含為一種可估計的值，它不是指具體的、確切的誤差值，雖可估計，但卻不能用以修正量值，只可在已修正測量結果的不確定度中考慮修正不完善而引入的不確定度；

而系統誤差的估計值如果已知則可以對測量結果進行修正，得到已修正的測量結果。

一個量值經修正後，可能會更靠近真值，但其不確定度不但不減小，有時反而會更大。這主要還是因為我們不能確切的知道真值為多少，僅能對測量結果靠近或離開真值的程度進行估計而已。

雖然測量不確定度與誤差有著以上種種不同，但它們仍存在著密切的聯繫。不確定度的概念是誤差理論的應用和拓展，而誤差分析依然是測量不確定度評估的理論基礎，在估計B類分量時，更是離不開誤差分析。例如測量儀器的特性可以用最大允許誤差、示值誤差等術語描述。在技術規範、規程中規定的測量儀器允許誤差的極限值，稱為“最大允許誤差”或“允許誤差限”。它是製造廠對某種型號儀器所規定的示值誤差的允許範圍，而不是某一台儀器實際存在的誤差。測量儀器的最大允許誤差可在儀器說明書中查到，用數值表示時有正負號，通常用絕對誤差、相對誤差、引用誤差或它們的組合形式表示。例如土0.1PV，土1%等。測量儀器的最大允許誤差不是測量不確定度，但可以作為測量不確定度評定的依據。測量結果中由測量儀器引入的不確定度可根據該儀器的最大允許誤差按B類評定方法評定。又如測量儀器的示值與對應輸入量的約定真值之差，為測量儀器的示值誤差。對於實物量具，示值就是其標稱值。通常用高一等級測量標準所提供的或復現的量值，作為約定真值(常稱校準值或標準值)。在檢定工作中，當測量標準給出的標準值的擴展不確定度為被檢儀器最大允許誤差的1/3～1/10時，且被檢儀器的示值誤差在規定的最大允許誤差內，則可判為合格。

抽樣推斷是按照隨機的原則從總體中抽取一部分單位進行觀察，並運用數理統計的原理，以被抽取的那部分單位的數量特徵為代表，根據觀察結果來推斷，對總體做出數量上的推斷分析。比如我們平時購買商品時，都要選一樣看看或者嘗一點試試，就可以知道全部商品是怎樣的，也就是說，你不必吃完整盤菜，才知道菜好不好吃。這是抽樣的精髓，從一部分得知全體。在抽樣的推斷中，要注意抽樣中的極限誤差與置信水平。

實際抽樣時，樣本的選取很關鍵。如果只抽取一個樣本，我們不知道從這個樣本得到的估計值與總體真正值的距離有多大，因為我們根本不知道總體真正值是多少。但是只要是從大的隨機樣本算出來的估計值，幾乎一定會靠近真正值。根據有多樣本結果構成的形態，我們可以知道用一個樣本的結果來估計總體時有多少置信程度。抽樣調查中的極限誤差，其實就是把抽樣的變異性換成調查結果置信程度的一種描述。變異性是說當抽取很多樣本時，統計量的值的離散程度。

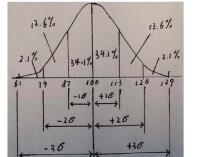
極限誤差通常是這樣描述的：極限誤差是正負3個百分點。它的意思是如果我們用同樣的抽樣方法抽取許多樣本，則這些樣本中有95%，其所得的結果會在總體真正值的正負3個百分點之內。通常一個隨機樣本的結果，不會剛好估計出總體的真正值，我們必須用一個極限誤差來描述估計值與總體真正值的距離，但是又不能百分之百確

定，估計值和總體真正值的差距必定小於極限誤差。所有樣本當中有95%，距離總體真正值的確有這麼近，但是另外的5%，距總體真正值的差距就超過極限誤差了。我們並不知道總體的真正值是多少，所以我們也無法得知，我們的樣本到底是屬於那95%的樣本還是屬於5%的樣本。所以我們只能說是有95%的可靠性，總體真正值會在極限誤差內。95%是我們通常所說的置信程度或者有95%的信心或者置信水平。

置信程度是估計的可靠程度。比如說調查發現有47%的女性認為她們沒有足夠的個人時間，我們有95%的信心，使所有女性的真正比率，會在這個樣本結果的正負3個百分點範圍內。這是關於置信程度的敘述。置信程度包含兩個內容：極限誤差和置信水平。極限誤差告訴我們，樣本統計量與總體參數的距離有多大，也就是估計的準確性。置信水平則告訴我們，所有可能樣本中有多少把握滿足這樣的極限誤差。置信程度顯示出所有可能樣本會發生的狀況，我們用它來描述對一個樣本的結果有多少可信程度。95%的置信程度的意思是如果我們用同樣的抽樣方法，有95%的時候可以得到與總體真正值這麼接近的結果。

有幾點需要說明：

（1）置信程度的結論永遠是針對總體而不是針對樣本。比如對女性問題的調查的置信程度是根據樣本結果來對所有女性這個總體做某種結論。

（2）對總體所做的結論永遠不會是完全正確的，你的樣本可能就是置信程度超過3個百分點的5%的樣本之一。

（3）抽樣推斷可以選擇95%以外的置信水平。抽樣中的極限誤差決定了估計的準確性，置信程度決定了估計的可靠性。在抽樣推斷中，總是希望估計的準確性盡量高一些，估計的可靠性盡量大一些，對於同一個總體來說，提高了估計的準確性必然會降低估計的可靠性，也就是說，較高的置信水平的代價是較大的極限誤差。對於同一個樣本，99%的置信程度的極限誤差，就比95%置信程度的要大，如果只要95%的置信程度，就可以得到較小的極限誤差。在估計時，只能對其中的一個要素提出要求，而推求另一個要素的變化情況。我們前面計算的極限誤差的簡單方法用的就是95%的置信程度。實際當中，應用95%的置信水平是很普遍的。

（4）如果對估計的可靠性提出要求，即在同樣的置信水平下，又要求較小的極限誤差來要求估計的準確性，就取一個大一點的樣本，因為較大的樣本會有較小的變異性，只要抽取較大的樣本，就可以得到所要求的小的極限誤差，並且仍然維持高的置信水平。