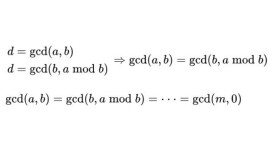歐幾里得演演算法
應用於數學和計算機領域的演演算法
歐幾里德演演算法又稱輾轉相除法,用於計算兩個整數a,b的最大公約數。
其計算原理依賴於下面的定理:
定理:gcd(a,b) = gcd(b,a mod b)
證明:a可以表示成a = kb + r ,則r = a mod b
假設d是a,b的一個公約數,則有
d|a, d|b,而r = a - kb,因此d|r
因此d是(b,a mod b)的公約數
假設d 是(b,a mod b)的公約數,則
d | b , d |r ,但是a = kb +r
因此d也是(a,b)的公約數
因此(a,b)和(b,a mod b)的公約數是一樣的,其最大公約數也必然相等,得證。
歐幾里德演演算法就是根據這個原理來做的,其演演算法用C++語言描述為:
void swap(int & a, int & b)
{
int c = a;
a = b;
b = c;
}
int gcd(int a,int b)
{
if(0 == a )
{
return b;
}
if( 0 == b)
{
return a;
}
if(a > b)
{
swap(a,b);
}
int c;
for(c = a % b ; c > 0 ; c = a % b)
{
a = b;
b = c;
}
return b;
}
對於整數a、p,如果存在整數b,滿足ab mod p =1,則說,b是a的模p乘法逆元。
定理:a存在模p的乘法逆元的充要條件是gcd(a,p) = 1
證明:
首先證明充分性
如果gcd(a,p) = 1,根據歐拉定理,aφ(p) ≡ 1 mod p,因此
顯然aφ(p)-1 mod p是a的模p乘法逆元。
再證明必要性
假設存在a模p的乘法逆元為b
ab ≡ 1 mod p
則ab = kp +1 ,所以1 = ab - kp
因為gcd(a,p) = d
所以d | 1
所以d只能為1
擴展歐幾里德演演算法不但能計算(a,b)的最大公約數,而且能計算a模b及b模a的乘法逆元,用C語言描述如下:
int gcd(int a, int b , int& ar,int & br)
{
int x1,x2,x3;
int y1,y2,y3;
int t1,t2,t3;
if(0 == a)
{//有一個數為0,就不存在乘法逆元
ar = 0;
br = 0 ;
return b;
}
if(0 == b)
{
ar = 0;
br = 0 ;
return a;
}
x1 = 1;
x2 = 0;
x3 = a;
y1 = 0;
y2 = 1;
y3 = b;
int k;
for( t3 = x3 % y3 ; t3 != 0 ; t3 = x3 % y3)
{
k = x3 / y3;
t2 = x2 - k * y2;
t1 = x1 - k * y1;
x1 = y1;
x1 = y2;
x3 = y3;
y1 = t1;
y2 = t2;
y3 = t3;
}
if( y3 == 1)
{
//有乘法逆元
ar = y2;
br = x1;
return 1;
}else{
//公約數不為1,無乘法逆元
ar = 0;
br = 0;
return y3;
}
}
擴展歐幾里德演演算法對於最大公約數的計算和普通歐幾里德演演算法是一致的。
首先重複拙作整除中的一個論斷:
如果gcd(a,b)=d,則存在m,n,使得d = ma + nb,稱呼這種關係為a、b組合整數d,m,n稱為組合係數。當d=1時,有 ma + nb = 1 ,此時可以看出m是a模b的乘法逆元,n是b模a的乘法逆元。
為了證明上面的結論,我們把上述計算中xi、yi看成ti的迭代初始值,考察一組數(t1,t2,t3),用歸納法證明:當通過擴展歐幾里德演演算法計算后,每一行都滿足a×t1 + b×t2 = t3
第一行:1 × a + 0 × b = a成立
第二行:0 × a + 1 × b = b成立
假設前k行都成立,考察第k+1行
對於k-1行和k行有
t1(k-1) t2(k-1) t3(k-1)
t1(k) t2(k) t3(k)
分別滿足:
t1(k-1) × a + t2(k-1) × b = t3(k-1)
t1(k) × a + t2(k) × b = t3(k)
根據擴展歐幾里德演演算法,假設t3(k-1) = j t3(k) + r
則:
t3(k+1) = r
t2(k+1) = t2(k-1) - j × t2(k)
t1(k+1) = t1(k-1) - j × t1(k)
則
t1(k+1) × a + t2(k+1) × b
=t1(k-1) × a - j × t1(k) × a +
t2(k-1) × b - j × t2(k) × b
= t3(k-1) - j t3(k) = r
= t3(k+1)
得證
因此,當最終t3迭代計算到1時,有t1× a + t2 × b = 1,
顯然,t1是a模b的乘法逆元,t2是b模a的乘法逆元。
其計算原理依賴於下面的定理:
定理:兩個整數的最大公約數等於其中較小的那個數和兩數相除餘數的最大公約數。最大公約數(Greatest Common Divisor)縮寫為GCD。
gcd(a,b) = gcd(b,a mod b) (不妨設a>b 且r=a mod b ,r不為0)
證法一
a可以表示成a = kb + r(a,b,k,r皆為正整數,且r
假設d是a,b的一個公約數,記作d|a,d|b,即a和b都可以被d整除。
而r = a - kb,兩邊同時除以d,r/d=a/d-kb/d,由等式右邊可知m=r/d為整數,因此d|r
因此d也是b,a mod b的公約數。
因(a,b)和(b,a mod b)的公約數相等,則其最大公約數也相等,得證。
證法二
假設c = gcd(a,b),則存在m,n,使a = mc, b = nc;
令r = a mod b,即存在k,使r = a-kb = mc - knc = (m-kn)c;
故gcd(b,a mod b) = gcd(b,r) = gcd(nc,(m-kn)c) = gcd(n,m-kn)c;
則c為b與a mod b的公約數;
假設d = gcd(n,m-kn), 則存在x,y, 使n = xd, m-kn = yd; 故m = yd+kn = yd+kxd = (y+kx)d;
故有a = mc = (y+kx)dc, b = nc = xdc; 可得 gcd(a,b) = gcd((y+kx)dc,xdc) = dc;
由於gcd(a,b) = c, 故d = 1;
即gcd(n,m-kn) = 1, 故可得gcd(b,a mod b) = c;
故得證gcd(a,b) = gcd(b,a mod b).
注意:兩種方法是有區別的。
Lemma 1.3.1 若 a,b 且 a = bh + r,其中 h,r,則 gcd(a,b) = gcd(b,r)。
證 明. 假設 d1 = gcd(a,b) 且 d2 = gcd(b,r),我們證明 d1| d2 且 d2| d1,因而可利用 Proposition 1.1.3⑵ 以及 d1,d2 皆為正數得證 d1 = d2。
因 d1| a 且 d1| b 利用 Corollary 1.1.2 我們知 d1| a - bh = r. 因為 d1| b,d1| r 且 d2 = gcd(b,r) 故由 Proposition 1.2.5 知 d1| d2. 另一方面,因為 d2| b 且 d2| r 故 d2| bh + r = a. 因此可得 d2| d1。
Lemma 1.3.1 告訴我們當 a > b > 0 時,要求 a,b 的最大公因數我們可以先將 a 除以 b 所得餘數若為 r,則 a,b 的最大公因數等於 b 和 r 的最大公因數. 因為 r < b < a,所以當然把計算簡化了,接著我們就來看看輾轉相除法. 由於 gcd(a,b) = gcd(- a,b) 所以我們只要考慮 a,b 都是正整數的情況。
Theorem 1.3.2 (The Euclidean Algorithm) 假設 a,b 且 a > b. 由除法原理我們知存在 h0,r0 使得
歐幾里得演演算法
a = bh0 + r0,其中 r0 < b.
若 r0 > 0,則存在 h1,r1 使得
b = r0h1 + r1,其中 0r1 < r0.
若 r1 > 0,則存在 h2,r2 使得
r0 = r1h2 + r2,其中 0r2 < r1.
如此繼續下去直到 rn = 0 為止,若 n = 0 (即 r0 = 0),則 gcd(a,b) = b. 若 n1,則 gcd(a,b) = rn - 1。
證 明. 首先注意若 r0 0,由於 r0 > r1 > r2 > ... 是嚴格遞減的,因為 r0 和 0 之間最多僅能插入 r0 - 1 個正整數,所以我們知道一定會有 nr0 使得 rn = 0。
若 r0 = 0,即 a = bh0,故知 b 為 a 之因數,得證 b 為 a,b 的最大公因數。若 r0 > 0,則由 Lemma 1.3.1 知
gcd(a,b) = gcd(b,r0) = gcd(r0,r1) = ... = gcd(rn - 1,rn) = gcd(rn - 1,0) = rn - 1。
現在我們來看用輾轉相除法求最大公因數的例子
Example 1.3.3 我們求 a = 481 和 b = 221 的最大公因數。首先由除法原理得 481 = 2 . 221 + 39,知 r0 = 39. 因此再考慮 b = 221 除以 r0 = 39 得 221 = 5 . 39 + 26,知 r1 = 26,再以 r0 = 39 除以 r1 = 26 得 39 = 1 . 26 + 13,知 r2 = 13。最後因為 r2 = 13整除r1 = 26 知 r3 = 0,故由 Theorem 1.3.2 知 gcd(481,221) = r2 = 13。
在利用輾轉相除法求最大公因數時,大家不必真的求到 rn = 0,例如在上例中可看出 r0 = 39 和 r1 = 26 的最大公因數是 13,利用 Lemma 1.3.1 馬上得知 gcd(a,b) = 13。
在上一節 Corollary 1.2.5 告訴我們若 gcd(a,b) = d,則存在 m,n 使得 d = ma + nb。當時我們沒有提到如何找到此 m,n,我們利用輾轉相除法來介紹一個找到 m,n 的方法,我們沿用 Theorem 1.3.2 的符號,看 r0 = 0 的情形,此時 d = gcd(a,b) = b 所以若令 m = 0,n = 1,則我們有 d = b = ma + nb. 當 r0 0 但 r1 = 0 時,我們知 d = gcd(a,b) = r0。故利用 a = bh0 + r0 知,若令 m = 1,n = - h0,則 d = r0 = ma + nb。同理若 r0 0,r1 0 但 r2 = 0,則知 d = gcd(a,b) = r1。故利用 a = bh0 + r0 以及 b = r0h1 + r1 知
r1 = b - r0h1 = b - (a - bh0)h1 = - h1a + (1 + h0h1)b。
歐幾里得演演算法(2張)
因此若令 m = - h1 且 n = 1 + h0h1,則 d = r1 = ma + nb. 依照此法,當 r0,r1 和 r2 皆不為 0 時,由於 d = gcd(a,b) = rn - 1 故由 rn - 3 = rn - 2hn - 1 + rn - 1 知 d = rn - 3 - hn - 1rn - 2. 利用前面推導方式我們知存在 m1,m2,n1,n2 使得 rn - 3 = m1a + n1b 且 rn - 2 = m2a + n2b 故代入得
d = (m1a + n1b) - hn - 1(m2a + n2b) = (m1 - hn - 1m2)a + (n1 - hn - 1n2)b.
因此若令 m = m1 - hn - 1m2 且 n = n1 - hn - 1n2,則 d = ma + nb.
上面的說明看似好像當 r0 0 時對每一個 i {0,1,...,n - 2} 要先將 ri 寫成 ri = mia + nib,最後才可將 d = rn - 1 寫成 ma + nb 的形式,其實這只是論證時的方便,在實際操作時我們其實是將每個 ri 寫成 mi'ri - 2 + ni'ri - 1 的形式慢慢逆推回 d = ma + nb. 請看以下的例子.
Example 1.3.4 我們試著利用 Example 1.3.3 所得結果找到 m,n 使得 13 = gcd(481,221) = 481m + 221n. 首先我們有 13 = r2 = 39 - 26 = r0 - r1. 而 r1 = 221 - 5 . 39 = b - 5r0,故得 13 = r0 - (b - 5r0) = 6r0 - b. 再由 r0 = 481 - 2 . 221 = a - 2b,得知 13 = 6(a - 2b) - b = 6a - 13b. 故得 m = 6 且 n = - 13 會滿足 13 = 481m + 221n。
要注意這裡找到的 m,n 並不會是唯一滿足 d = ma + nb 的一組解,雖然上面的推演過程好像會只有一組解,不過只能說是用上面的方法會得到一組解,並不能擔保可找到所有的解,比方說若令 m' = m + b,n' = n - a,則 m'a + n'b = (m + b)a + (n - a)b = ma + nb = d. 所以 m',n' 也會是另一組解,所以以後當要探討唯一性時,若沒有充分的理由千萬不能說由前面的推導過程看出是唯一的就斷言是唯一,一般的作法是假設你有兩組解,再利用這兩組解所共同滿足的式子找到兩者之間的關係. 我們看看以下的作法。
Proposition 1.3.5 假設 a,b 且 d = gcd(a,b)。若 x = m0,y = n0 是 d = ax + by 的一組整數解,則對任意 t,x = m0 + bt/d,y = n0 - at/d 皆為 d = ax + by 的一組整數解,而且 d = ax + by 的所有整數解必為 x = m0 + bt/d,y = n0 - at/d 其中 t 這樣的形式。
證 明. 假設 x = m,y = n 是 d = ax + by 的一組解,由於已假設 x = m0,y = n0 也是一組解,故得 am + bn = am0 + bn0. 也就是說 a(m - m0) = b(n0 - n). 由於 d = gcd(a,b),我們可以假設 a = a'd,b = b'd 其中 a',b' 且 gcd(a',b') = 1 (參見 Corollary 1.2.3)。因此得 a'(m - m0) = b'(n0 - n)。利用 b'| a'(m - m0),gcd(a',b') = 1 以及 Proposition 1.2.7⑴ 得 b'| m - m0. 也就是說存在 t 使得 m - m0 = b't. 故知 m = m0 + b't = m0 + bt/d. 將 m = m0 + bt/d 代回 am + bn = am0 + bn0 可得 n = n0 - at/d,因此得證 d = ax + by 的整數解都是 x = m0 + bt/d,y = n0 - at/d 其中 t 這樣的形式. 最後我們僅要確認對任意 t,x = m0 + bt/d,y = n0 - at/d 皆為 d = ax + by 的一組整數解,然而將 x = m0 + bt/d,y = n0 - at/d 代入 ax + by 得 a(m0 + bt/d)+ b(n0 - at/d)= am0 + bn0 = d,故得證本定理。
利用 Proposition 1.3.5 我們就可利用 Example 1.3.4 找到 13 = 481x + 221y 的一組整數解 x = 6,y = - 13 得到 x = 6 + 17t,y = - 13 - 37t 其中 t 是 13 = 481x + 221y 所有的整數解。
輾轉相除法是利用以下性質來確定兩個正整數 a 和 b 的最大公因子的:
⒈ 若 r 是 a ÷ b 的餘數,且r不為0,則
gcd(a,b) = gcd(b,r)
⒉ a 和其倍數之最大公因子為 a。
另一種寫法是:
⒈ 令r為a/b所得餘數(0≤r
若 r= 0,演演算法結束;b 即為答案。
⒉ 互換:置 a←b,b←r,並返回第一步。
Swift 語言版本
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | import Foundation func gcd(a: Int, b: Int) -> Int { var x = a, y = b while y != 0 { (x, y) = (y, x % y) } return x } let x = 75, y = 100 let result = gcd(a: x, b: y) print("\(x) 和 \(y) 的最大公約數是 \(result)") |
Go語言版本
1 2 3 4 5 6 7 8 9 10 11 12 13 | package main import "fmt" func main() { var x, y int = 18, 12 result := gcd(x,y) fmt.Printf("x, y 的最大公約數是 : %d",result) } func gcd(x,y int) int{ for y != 0 { x, y = y, x%y } return x } |
Pascal語言版
1 2 3 4 5 6 7 8 9 10 | var a,b,c:integer; begin readln(a,b); c:=a mod b; while c<>0 do begin a:=b;b:=c;c:=a mod b; end; write(b); end. |
C語言版
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | #include unsigned int MaxCommonFactor(int a,int b) { if(b<=0) return a; return MaxCommonFactor(b,a%b); } unsigned int Gcd(unsigned int M,unsigned int N) { unsigned int Rem; while(N > 0) { Rem = M % N; M = N; N = Rem; } return M; } int main(void) { int a,b; scanf("%d %d",&a,&b); printf("the greatest common factor of %d and %d is ",a,b); printf("%d\n",Gcd(a,b)); printf("recursion:%d\n",MaxCommonFactor(a,b)); return 0; } |
Ruby語言版
1 2 3 4 5 6 7 8 | #用歐幾里得演演算法計算最大公約數(排版略) def gcd(x, y) if y == 0 return x else return gcd(y, x % y) end end |
C++版
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | #include using namespace std; int gcd(int a, int b) { if (a < b) swap(a, b); return b == 0 ? a : gcd(b, a % b); } int x, y; int main(){ cin >> x >> y; cout << gcd(x, y); return 0; } |
Java版
1 2 3 4 5 6 7 | int gcd(int m,int n) { if(n == 0){ return m; } int r = m%n; return gcd(n,r); } |
JavaScript版
1 2 3 4 | function gcd(a, b) { if (a % b == 0) return b; return gcd(b, a % b); } |
Python版
1 2 3 4 5 6 | def gcd(a, b): while a != 0: a, b = b % a, a return b |
Erlang版
1 2 | gcd(A, 0) -> A; gcd(A, B) -> gcd(B, A rem B). |
Rust版
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 | pub fn gcd(x: u64, y: u64) -> u64 { let remainder = x % y; if remainder == 0 { return y; } else { return gcd(y, remainder); } } #[cfg(test)] mod tests { use super::*; #[test] fn gcd_works() { assert_eq!(gcd(2, 4), 2); assert_eq!(gcd(6, 27), 3); assert_eq!(gcd(4, 2), 2); assert_eq!(gcd(27, 6), 3); } } |
Bash版
1 2 3 4 5 6 7 8 9 10 | function gcd() { if [ ! -n "$2" ];then return fi if [ "$2" == "0" ];then echo "$1" return fi gcd "$2" "$[$1%$2]" } |
模P乘法逆元
對於整數a、p,如果存在整數b,滿足ab mod p =1,則說,b是a的模p乘法逆元。
定理:a存在模p的乘法逆元的充要條件是gcd(a,p) = 1
證明:
首先證明充分性
如果gcd(a,p) = 1,根據歐拉定理,aφ(p) ≡ 1 mod p,因此
顯然aφ(p)-1 mod p是a的模p乘法逆元。
再證明必要性
假設存在a模p的乘法逆元為b
ab ≡ 1 mod p
則ab = kp +1 ,所以1 = ab - kp
因為gcd(a,p) = d
所以d | 1
所以d只能為1
Stein演演算法
歐幾里得演演算法是計算兩個數最大公約數的傳統演演算法,他無論從理論還是從效率上都是很好的。但是他有一個致命的缺陷,這個缺陷只有在大素數時才會顯現出來。
硬體平台,一般整數最多也就是64位,對於這樣的整數,計算兩個數之間的模是很簡單的。對於字長為32位的平台,計算兩個不超過32位的整數的模,只需要一個指令周期,而計算64位以下的整數模,也不過幾個周期而已。但是對於更大的素數,這樣的計算過程就不得不由用戶來設計,為了計算兩個超過 64位的整數的模,用戶也許不得不採用類似於多位數除法手算過程中的試商法,這個過程不但複雜,而且消耗了很多CPU時間。對於現代密碼演演算法,要求計算 128位以上的素數的情況比比皆是,設計這樣的程序迫切希望能夠拋棄除法和取模。
Stein演演算法由J. Stein於1961年提出,這個方法也是計算兩個數的最大公約數。和歐幾里得演演算法不同的是,Stein演演算法只有整數的移位和加減法,這對於程序設計者是一個福音。
為了說明Stein演演算法的正確性,首先必須注意到以下結論:
gcd(a,a) = a,也就是一個數和他自身的公約數是其自身
gcd(ka,kb) = k gcd(a,b),也就是最大公約數運算和倍乘運算可以交換,特殊的,當k=2時,說明兩個偶數的最大公約數必然能被2整除
C++/java 實現
// c++/java stein 演演算法
int gcd(int a,int b)
{if(ab
{int temp = a;a = b;b=temp;}
if(0==b) //the base case
return a;
if(a%2==0 && b%2 ==0) //a and b are even
return 2*gcd(a/2,b/2);
if (a%2 == 0) // only a is even
return gcd(a/2,b);
if (b%2==0)// only b is even
return gcd(a,b/2);
return gcd((a-b)/2,b);// a and b are odd
}
演演算法擴展
擴展歐幾里得演演算法不但能計算(a,b)的最大公約數,而且能計算a模b及b模a的乘法逆元,用C語言描述如下:
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 | #include unsigned int gcdExtended( int a, int b, int *x, int *y); int main(void) { int a, b,GCD; int x, y; a = 1232, b = 573; GCD = gcdExtended(a, b,&x, &y); printf("gcdExtended(%d, %d) = %d, x=%d, y=%d\n", a, b, GCD,x,y); return 0; } // 歐幾里得擴展演演算法的C語言實現 // ax+by=1 unsigned int gcdExtended(int a, int b, int *x, int *y){ if (a == 0){ *x = 0; *y = 1; return b; } int x1, y1; int gcd = gcdExtended(b%a, a, &x1, &y1); *x = y1 - (b/a) * x1; *y = x1; return gcd; } |
擴展歐幾里得演演算法對於最大公約數的計算和普通歐幾里得演演算法是一致的。計算乘法逆元則顯得很難明白。我想了半個小時才想出證明他的方法。
首先重複拙作整除中的一個論斷:
為了證明上面的結論,我們把上述計算中xi、yi看成ti的迭代初始值,考察一組數(t1,t2,t3),用歸納法證明:當通過擴展歐幾里得演演算法計算后,每一行都滿足a×t1 + b×t2 = t3
第一行:1 × a + 0 × b = a成立
第二行:0 × a + 1 × b = b成立
假設前k行都成立,考察第k+1行
對於k-1行和k行有
t1(k-1) t2(k-1) t3(k-1)
t1(k) t2(k) t3(k)
分別滿足:
t1(k-1) × a + t2(k-1) × b = t3(k-1)
t1(k) × a + t2(k) × b = t3(k)
根據擴展歐幾里得演演算法,假設t3(k-1) = j t3(k) + r
則:
t3(k+1) = r
t2(k+1) = t2(k-1) - j × t2(k)
t1(k+1) = t1(k-1) - j × t1(k)
則
t1(k+1) × a + t2(k+1) × b
=t1(k-1) × a - j × t1(k) × a +
t2(k-1) × b - j × t2(k) × b
= t3(k-1) - j t3(k) = r
= t3(k+1)
得證
因此,當最終t3迭代計算到1時,有t1× a + t2 × b = 1,顯然,t1是a模b的乘法逆元,t2是b模a的乘法逆元。