共找到2條詞條名為伴隨矩陣的結果 展開
- 線性代數術語
- 伴隨陣
伴隨矩陣
線性代數術語
在線性代數中，一個方形矩陣的伴隨矩陣（英語：adjugate matrix）是一個類似於逆矩陣的概念。如果矩陣可逆，那麼它的逆矩陣和它的伴隨矩陣之間只差一個係數。然而，伴隨矩陣對不可逆的矩陣也有定義，並且不需要用到除法。A的伴隨矩陣記作adj(A)，或A*。
設R是一個交換環，A是一個以R中元素為係數的n×n的矩陣。A的伴隨矩陣可按如下步驟定義：
定義：A關於第i行第j列的餘子式（記作Mᵢⱼ）是去掉A的第i行第j列之後得到的(n−1)×(n−1)矩陣的行列式。
定義：A關於第i行第j列的代數餘子式是：
Cᵢⱼ=(−1)ⁱ⁺ʲMᵢⱼ。
定義：A的餘子矩陣是一個n×n的矩陣C，使得其第i行第j列的元素是A關於第i行第j列的代數餘子式。
引入以上的概念后，可以定義：矩陣A的伴隨矩陣是A的餘子矩陣的轉置矩陣：
adj(A)=Cᐪ，
也就是說，A的伴隨矩陣是一個n×n的矩陣（記作adj(A)），使得其第i行第j列的元素是A關於第j行第i列的代數餘子式。簡言之，伴隨矩陣就是把原來矩陣每一行的代數餘子式豎著寫：
[adj(A)]ᵢⱼ=Cⱼᵢ。
2x2矩陣：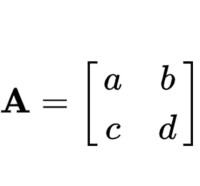
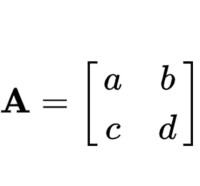
伴隨矩陣
它的伴隨矩陣：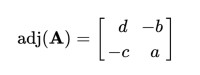
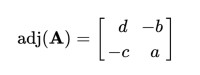
伴隨矩陣
對於3x3的矩陣，情況稍微複雜一點：
伴隨矩陣
其伴隨矩陣是：
伴隨矩陣
其中
伴隨矩陣
要注意伴隨矩陣是餘子矩陣的轉置，因此第3行第2列的係數是A關於第2行第3列的代數餘子式。
對於數值矩陣，例如求矩陣的伴隨矩陣adj(A)，只需將數值代入上節得到的表達式中。即：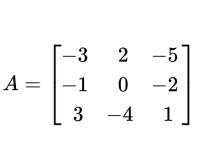
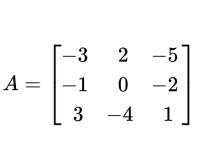
伴隨矩陣
只需將數值代入上節得到的表達式中。
即：adj(A)ⱼᵢ=Cᵢⱼ=（−1）ⁱ⁺ʲ(Mᵢⱼ)。
其中，Mᵢⱼ為刪掉矩陣 {\displaystyle A} 的第i橫列與第j縱行后得到的行列式，Cⱼᵢ為矩陣A的余因子。
例如adj(A)中第3行第2列的元素為
伴隨矩陣
依照其順序一一計算，便可得到計算后的結果是：
伴隨矩陣
作為拉普拉斯公式的推論，關於n×n矩陣A的行列式，有：
A adj(A)=adj(A)A=det(A)I（⁎）
其中I是n階的單位矩陣。事實上，A adj(A)的第i行第i列的係數是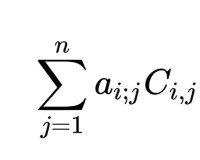
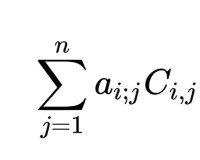
伴隨矩陣
根據拉普拉斯公式，等於A的行列式。
如果i ≠ j，那麼A adj(A)的第i行第j列的係數是
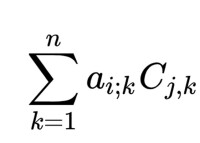
伴隨矩陣
拉普拉斯公式說明這個和等於0（實際上相當於把A的第j行元素換成第i行元素后求行列式。由於有兩行相同，行列式為0）。
由這個公式可以推出一個重要結論：交換環R上的矩陣A可逆當且僅當其行列式在環R中可逆。
這是因為如果A可逆，那麼
1=det(I)=det(A A⁻¹)=det(A⁻¹)
如果det(A)是環中的可逆元那麼公式（*）表明
A⁻¹=det(A)⁻¹adj(A)
對n×n的矩陣A和B，有：
1.adj(I)=I
2.adj(AB)=adj(B)adj(A)
3.adj(Aᐪ)=adj(A)ᐪ
4.det(adj(A))=det(A)ⁿ⁻¹
5.adj(kA)=kⁿ⁻¹adj(A)
6.當n>2時，adj(adj(A))=(det A)ⁿ⁻²A
7.如果A可逆，那麼adj(A)⁻¹=adj(A)⁻¹=A/detA
8.如果A是對稱矩陣，那麼其伴隨矩陣也是對稱矩陣；如果A是反對稱矩陣，那麼當n為偶數時，A的伴隨矩陣也是反對稱矩陣，n為奇數時則是對稱矩陣。
9.如果A是（半）正定矩陣，那麼其伴隨矩陣也是（半）正定矩陣。
10.如果矩陣A和B相似，那麼adj(A)和adj(B)也相似。
11.如果n>2，那麼非零矩陣A是正交矩陣當且僅當adj(A)=±Aᐪ
當矩陣A可逆時，它的伴隨矩陣也可逆，因此兩者的秩一樣，都是n。當矩陣A不可逆時，A的伴隨矩陣的秩通常並不與A相同。當A的秩為n-1時，其伴隨矩陣的秩為1，當A的秩小於n-1時，其伴隨矩陣為零矩陣。
設矩陣A在復域中的特徵值為λ₁，λ₂…λₙ(即為特徵多項式的n個根），則A的伴隨矩陣的特徵值為
λ₂λ₃…λₙ，λ₁λ₃…λₙ，…，λ₁λ₂…λₙ₋₁。
設p(t)=det(A-tI)為A的特徵多項式，定義q(t)=(p(0)-p(t))/t，那麼：
adj(A)=q(A)=-(p₁I+p₂A+p₃A²+…+pₙAⁿ⁻¹)，
其中pᵢ是p(t)的各項係數：
p(t)=p₀+p₁t+p₂t² +…pₙtⁿ。
伴隨矩陣也出現在行列式的導數形式中。
基本信息
- 中文名
- 伴隨矩陣
- 外文名
- adjugate matrix
- 適用領域
- 線性代數
- 本質
- 類似於逆矩陣的概念
- 特點
- 逆矩陣和伴隨矩陣只差一個係數
- 性質
- 與原矩陣形成映射