邏輯代數

邏輯代數是分析和設計邏輯電路的數學基礎。邏輯代數是由英國科學家喬治·布爾(George·Boole)創立的，故又稱布爾代數。

當邏輯代數的邏輯狀態多於2種時（如0、1、2或更多狀態時），其通用模型的基本邏輯有2個。

一個是從一種狀態變為另一種狀態的邏輯，是一個一元邏輯；

另外一種是兩種狀態中按照某種規則（比如比較大小）有傾向性的選擇出其中一種狀態的邏輯，這是一個二元邏輯。

依據這兩種邏輯，可以表達任意多狀態的任意邏輯關係，即最小表達式。

即任意多狀態的邏輯是完備的。

當邏輯狀態數擴展有理數量級甚至更多。任意數學運算都可以用兩個運算關係來聯合表達：加減法和比較大小。邏輯代數，亦稱布爾代數，是英國數學家喬治 布爾（George Boole）於1849年創立的。在當時，這種代數純粹是一種數學遊戲，自然沒有物理意義，也沒有現實意義。在其誕生100多年後才發現其應用和價值。

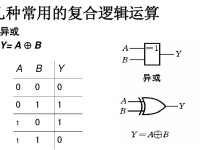
邏輯代數是按一定的邏輯關係進行運算的代數，是分析和設計數字電路的數學工具。在邏輯代數，只有0和1兩種邏輯值，有與、或、非三種基本邏輯運算，還有與或、與非、與或非、異或幾種導出邏輯運算。

邏輯是指事物的因果關係，或者說條件和結果的關係，這些因果關係可以用邏輯運算來表示，也就是用邏輯代數來描述。事物往往存在兩種對立的狀態，在邏輯代數中可以抽象地表示為 0 和 1 ，稱為邏輯0狀態和邏輯1狀態。

邏輯代數中的變數稱為邏輯變數，用大寫字母表示。邏輯變數的取值只有兩種，即邏輯0和邏輯1，0 和 1 稱為邏輯常量，並不表示數量的大小，而是表示兩種對立的邏輯狀態。

其規定：

1．所有可能出現的數只有0和1兩個。

2．基本運算只有“與”、“或”、“非”三種。

與運算（邏輯與、邏輯乘）定義為：

或運算（邏輯或、邏輯加）定義為：

至此布爾代數宣告誕生。

二、基本公式

如果用字母來代替數（字母的取值非0即1），根據布爾定義的三種基本運算，我們馬上可推出下列基本公式：

上述公式的證明可用窮舉法。如果對字母變數所有可能的取值，等式兩邊始終相等，該公式即告成立。

與邏輯和乘法

乘法原理中自變數是因變數成立的必要條件，與邏輯的定義正好和乘法原理的描述一致，所以與邏輯和乘法對應。

或邏輯和加法

加法原理中自變數是因變數成立的充分條件，或邏輯的定義正好和加法原理的描述一致，所以或邏輯和加法對應。

乘法就是廣義的與邏輯運算，加法就是廣義的或邏輯運算。邏輯運算可以看作是乘法的特例。邏輯推算推算可以看作是加法的特例。

總之，乘法原理、加法原理可以看作是一種邏輯和或邏輯的定量表述；與邏輯和或邏輯可以看作是乘法原理、加法原理的定性表述。

任何一個含有變數 X 的等式，如果將所有出現 X 的位置，都代之以一個邏輯函數 F，此等式仍然成立。

設 F 是一個邏輯函數式，如果將 F 中的所有的 * 變成 +，+ 變成 *，0 變成 1，1 變成 0，而變數保持不變。那麼就得到了一個邏輯函數式 F'，這個 F' 就稱為 F 的對偶式。如果用兩個函數 和 G 相等，則是它們各自的對偶式F' 和 G' 也相等。

當已知一個邏輯函數F，要求 ¬F 時，只要把 F 中的所有 * 變成 +，+ 變成 *，0 變成 1，1 變成 0，原變數變成反變數，反變數變成原變數，即得 ¬F。運用反演規則時必須注意一下兩個原則：（1）保持原來的運算優先順序，即先進行與運算，後進行或運算。並注意優先考慮括弧內的運算。（2）對於反變數以外的非號應保留不變。。

邏輯變數的邏輯與運算叫做與項，與項的邏輯或運算構成了邏輯函數的與或式，也叫做積之和式（SP form）。

邏輯變數的邏輯或運算叫做或項，或項的邏輯與運算構成了邏輯函數的或與式，也叫做和之積式(PS form)。

在n變數邏輯函數中，若m為包含n個因子的乘積項，而且n個變數均以原變數或反變數的形式在m中出現一次，則稱m為該組變數的最小項。

性質：

①在輸入變數的任何一取值下必有一個最小項，而且僅有一個最小項的值為1。

②任意兩個最小項的乘積為0。

③全體最小項之和為1。

④具有相鄰性的兩個最小項之和可以合併為一項並消去一個因子。

⑤n個變數的最小項數目為2n

在n變數邏輯函數中，若M為n個變數的和，而且這n個變數均以原變數或反變數的形式在M中出現一次，則稱M為該組變數的最大項。

性質：

①在輸入變數的任何取值下，必有一個，而且只有一個最大項的值是0。

②任意兩個最大項之和為1。

③全體最大項之積為0。

④只有一個變數不同的兩個最大項的乘積等於各相同變數之和。

⑤ n個變數的最大項數目為2n。

運用邏輯代數的基本公式及規則可以對邏輯函數進行變換，從而得到表達式的最簡形式。這裡所謂的最簡形式是指最簡與或式或者是最簡或與式，它們的判別標準有兩條：⑴項數最少；⑵在項數最少的條件下，項內的文字最少。

卡諾圖是遵循一定規律構成的。由於這些規律，使邏輯代數的許多特性在圖形上得到形象而直觀的體現，從而使它成為公式證明、函數化簡的有力工具。

類代數類代數是類邏輯的代數化。所謂類邏輯是從外延上理解的一階一元謂詞的邏輯。一元謂詞的外延指稱該謂詞所適用的個體的類。由論域中所有個體組成的類叫全類，記作 1。不含有任何事物的類叫空類，記作0。考慮全類的所有子類，即包含於其中的類（包括1和0），令…為這樣的類變元。由論域中不屬於a類的個體組成的類叫做a的補，記作a'。由或屬於a類或屬於b類的個體組成的類叫做a與b的邏輯和（並類），記作。由既屬於 a類又屬於 b類的個體組成的類叫做a與b的邏輯積（交類），記作，簡記作。如果a類與b類所含的個體相同，則稱a與b等同，記作。a與b不等同記作。1和0是兩個特定的類常元。'，∪和∩是三種邏輯運算，分別叫類的取補、求和（加法）和求積（乘法）。此外，還可以通過定義引入包含於關係吇，例如把a吇b定義為。於是自然有：對於任何類a,0吇a吇1。

在類代數中，不帶有主詞存在斷定的直言命題和，可表示為和。傳統邏輯中三段論第1格 AAA式可表示為：

如果且，則。第3格EIO式可表示為：

如果且，則。類代數的運算滿足下表中列出的基本定律。

類代數的基本定律

冪等律

交換律

結合律

吸收律

分配律

么元律

補余律

從這些定律出發，特別是只需以其中的交換律、分配律、前兩個么元律和補余律作為初始定律即公理，就可以推導出類邏輯的所有定律（定理）。類邏輯的內容比傳統的三段論理論要豐富得多，大致相當於只包含一元謂詞的一階謂詞邏輯（見謂詞邏輯）。一般的謂詞邏輯也可以用更進一步的代數方法處理，但已超出通常所謂的邏輯代數的範圍。

命題代數命題代數在結構上與類代數完全相同。只要對類代數中的符號另作命題邏輯的解釋，或者乾脆改為相應的命題邏輯符號，就得到命題代數。即把類變元改為命題變元；改為否定詞填（“並非”）；∪改為析取詞∨（“或者”）；∩改為合取詞∧（“並且”）。1和0分別解釋為特定的邏輯上真的命題和邏輯上假的命題，或稱有效命題和矛盾命題；=表示兩命題邏輯上等值。這時，填、∨和∧作為命題運算正好滿足形式上與類代數的基本定律相對應的定律，而整個命題代數可包括命題邏輯的全部內容。命題代數和類代數可以有各種形式的公理系統，尤其是都可以有關於布爾展開式的定理，它相當於命題邏輯中的優析取範式和優合取範式的定理。

邏輯代數與命題代數有所不同。它還可以把1和0分別解釋為命題的真和假，令變元只取1和0為值，即令其為二值的真值變元，並把填、∨和∧解釋為真值運算，從而得到一種提供命題真值運算定律的真值代數。而且，在二值的真值代數中特別可以有定理“或，但在一般的命題代數和類代數中卻沒有與此相應的定理。