四維空間

在物理學中描述物質變化時所需的參數，這個參數就叫做維。幾個參數就是幾個維。比如描述“門”的位置就只需要角度，所以是一維的而不是二維。

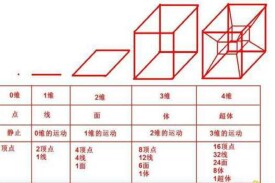
簡單地說：零維是點，沒有長度、寬度及高度。一維是由無數的點組成的一條線，只有長度，沒有其中的寬度、高度。二維是由無數的線組成的面，有長度、寬度沒有高度。三維是由無數的面組成的體，有長度、寬度、高度。

因為人的眼睛只能看到二維，二維生物看對方只有一條線。人的雙眼看到的是兩個二維投影，經過大腦處理形成一個整體的視覺。

一個簡單的說法：N維就是兩個以上的N-1維物體垂直所形成的空間。

1維的線，由1-1=0維的點均分；2維的面，由2-1=1維的線相互垂直均分；3維的空間，由3-1=2維的平面相互垂直均分。

因為，人類只能理解3維，所以後面的維度可以通過數學理論構建，但要仔細理解就很難。在量子力學，仍在建立的弦理論，認為世界是11維的。（十維空間+一維時間）

首先，錯誤的說法是把”四維空間定義為三維空間+時間軸”，而”三維空間+時間維”是另一種說法。前者也並非是什麼四維時空，而且本身四維時空是個偽概念。很簡單“時間只是因為粒子運動、宇宙膨脹而出現的概念，為什麼它就能成為第四維”

另外，時空和四維空間的概念是有區別的

將四維空間定義為三維空間+時間軸的說法是對於閔可夫斯基空間（ Minkowski space）這個概念的誤解，而為什麼這個誤解這麼廣泛呢？很簡單，無數科幻小說甚至於科普讀物刻意去硬生生地套用了這麼一個東西，造成廣泛的讀者影響。其中這個裡面涉及到了一組四維矢量場，也就是：

四維矢量依據它們（閔可夫斯基）內積的正負號來區分。可分類如下：

• 是類時(timelike)，

• 是類空(spacelike)，

• 是零(null)或稱類光(lightlike)，

然而，

關於零矢量一個有用的結果：“若兩個零矢量、正交（即：零內積值），則它們必定是呈比例關係（為常數）。”

以上的零基底部的時間方向選定，以及類時向量的概念，讓很多人誤以為“空間和時間組成了另一個空間”，而實際上上面只是描述了時間和空間的協同作用罷了。這便是前面那個說法的來源。

而實際上時間維是一種替代說法，並不是說第四個維度是時間，和前面那種說法並非一回事，第四維在主流的說法中具有連續性，著名的數學模型克萊因瓶，第四維穿過三維這個本質多面體，但四維空間的本質還是空間。而為什麼這一維會定義為時間維度呢，是因為某一派觀點認為廣延的“時間”具有空間性，故而出現的一種替代說法，你要將它叫什麼其實都可以，它是一個統一，確定的定義概念下產生的依據不同學派自主概念的命名法。

有些同學有點糾結於“時空”這個說法，我先說，沒有四維時空這種說法還有另一個理由，也就是時空在近代物理學中的概念本來就是四維的，所以不會冒出五維時空，也不存在時空前面特別說明為四維。近代物理學某一派認為，時間空間相互且可變，且其變數互相存於其中，而他們在特定條件下所對應的這一個廣域叫做時空（最早的人確實將時空等同於空間加時間軸，現在更多在避開這種本初定義），時空可能受到物質和能量的影響發生扭曲或者凹陷，且其最小單位是普朗克時間和普朗克長度。這是這個概念的由來，但是很多人把時空和四維空間混用，這兩者有相關性，但不能混用。

所以四維就是四個有聯繫的抽象概念組成的，第四個抽象概念是 實時間，第四聯繫值為速度。

高維度時空和高維度空間是不同的。舉例來說，在三維空間中只有一個時間維度，但它是一個偽維度，即它的單位和其他三個維度不同。四維空間的第四維仍然和三維空間的維度具有相同性質，時間仍是偽維度。因此，不可把時空和空間混為一談。

從廣義上講：維度是事物“有聯繫”的抽象概念的數量，“有聯繫”的抽象概念指的是由兩個抽象概念聯繫而成的抽象概念，如面積。所以四維就是四個有聯繫的抽象概念組成的，第四個抽象概念是實時間，第四聯繫值為速度。

摘要

幾何不一定是真實現象的描述，幾何空間和自然空間並不能完全等同看待，純概念的研究幾何的發展是數學界的一個里程碑。從零維空間到三維空間，尤其是從三維空間到四維空間的發展更是幾何學的的一次革命。

關鍵詞

零維；一維；二維；三維；四維；n維；幾何元素；點；直線；平面。

n維空間概念，在18世紀隨著分析力學的發展而有所前進。在達朗貝爾。歐拉和拉格朗日的著作中無關緊要的出現第四維的概念，達朗貝爾在《百科全書》關於維數的條目中提議把時間想象為第四維。在19世紀高於三維的幾何學還是被拒絕的。麥比烏斯（karl august mobius 1790-1868）在其《重心的計算》中指出，在三維空間中兩個互為鏡像的圖形是不能重疊的，而在四維空間中卻能疊合起來。但後來他又說：這樣的四維空間難於想象，所以疊合是不可能的。這種情況的出現是由於人們把幾何空間與自然空間完全等同看待的結果。以至直到1860年，庫摩爾（ernst eduard kummer 1810-1893）還嘲笑四維幾何學。但是，隨著數學家逐漸引進一些沒有或很少有直接物理意義的概念，例如虛數，數學家們才學會了擺脫“數學是真實現象的描述”的觀念，逐漸走上純觀念的研究方式。虛數曾經是很令人費解的，因為它在自然界中沒有實在性。把虛數作為直線上的一個定向距離，把複數當作平面上的一個點或向量，這種解釋為後來的四元數，非歐幾里得幾何學，幾何學中的復元素，n維幾何學以及各種稀奇古怪的函數，超限數等的引進開了先河，擺脫直接為物理學服務這一觀念迎來了n維幾何學。

1844年格拉斯曼在四元數的啟發下，作了更大的推廣，發表《線性擴張》，1862年又將其修訂為《擴張論》。他第一次涉及一般的n維幾何的概念，他在1848年的一篇文章中說：

我的擴張的演算建立了空間理論的抽象基礎，即它脫離了一切空間的直觀，成為一個純粹的數學的科學，只是在對（物理）空間作特殊應用時才構成幾何學。

然而擴張演算中的定理並不單單是把幾何結果翻譯成抽象的語言，它們有非常一般的重要性，因為普通幾何受（物理）空間的限制。格拉斯曼強調，幾何學可以物理應用發展純智力的研究。幾何學從此開始割斷了與物理學的聯繫而獨自向前發展。

經過眾多的學者的研究，遂於1850年以後，n維幾何學逐漸被數學界接受。

四維空間的概念也可以通過解析幾何的手段來研究。在那裡我們可以利用代數方程來表示幾何概念。為了利用這個手段進行觀察以導致對四維空間的理解，我們來研究三維空間體系中的三個幾何元素——點、直線和平面的方程。利用笛卡爾系統表示，我們可以寫出：

點的方程：ax + b = 0 （坐標系：直線上的一個點）。

直線的方程：ax + by + c = 0 （坐標系：平面上的兩條正交直線）。

平面的方程：ax + by + cz + d = 0 (坐標系：三維空間的三個互相垂直的平面)。

從上面的研究我們可以看出：

所表示的每一個幾何元素（或空間）的方程中的變數數目，等於這個空間的維數加1。

坐標系中的幾何元素與被表示的幾何空間的幾何元素的維數相同。

在這個坐標系中，幾何元素的數目等於被表示的空間的維數加1。在坐標系中，幾何元素的這個數目是最低要求。

用來表示幾何元素的坐標系，位於比它所含有的幾何元素高一維的空間里。

根據上述觀察，我們可以寫出三維空間的下述方程。應當注意：這個方程有四個變數（x、y、z、u）。

ax + by + cz + du + e = 0

根據這公式我們可以斷定：

1. 這個坐標系的幾何元素有三維，即它們是三維空間。

2. 在這個坐標系中有四個三維空間。

3. 這個坐標系位於一個四維空間里。

我們對於四維空間乃至更高空間的研究，不是通過實驗總結的方式，在現實中我們很難發現並推導出它們的一般規律，對於這些問題，我們可以採取一種新的研究方式。即：純概念的研究。通過這種方式，我們可以容易的推導出這些很重要但在現實中不易想象的新內容。

如果一個三維空間的東西，當他的密度為負值時，是否會變成四維空間的事物呢？

對於四維空間，人們普遍認為空間有軸對稱性，或是中心對稱。譬如，倘若一個三維空間的人進入四維空間，並且按照適當的方式“旋轉”一下再回到三維空間，那麼他會被‘軸對稱’一下（這在三維空間中當然是不可能實現的，除非運用三維版本的麥比烏斯帶）。當然，由於沒有人進入四維空間，所以這只是一個從二維空間類比而得的假設，無法進行驗證。但是關於時間軸的觀點以及時空錯亂瞬間的現象與這是相符的。

從二維空間的一個圖形是不能在二維空間進行對稱的，但進入三維空間，就可以通過進行翻轉回到二維空間時，就可以實現對稱，因為在二維空間是不能進行翻轉的，只能旋轉或平移。因此我們可以推測三維物體進入了四維空間，再回到三維空間可能物體會被“軸對稱”一下。

一般人說到“四維空間”時，經常是誤指愛因斯坦在他的廣義相對論和狹義相對論中提及的四維時空（叫做閔可夫斯基時空）概念。

這種普遍性的誤用，是由於相對論的相關科普和文藝作品的流行。

關於這一點，考克斯特曾寫道：

把時間作為第四維數帶來的好處，即使有也微不足道。實際上，H. G. 威爾斯在《時間機器》中發展的這種十分吸引人的觀點導致了J. W. 杜恩（《時間實驗》）等作者對相對論有非常錯誤的理解。閔可夫斯基的時空幾何是不符合歐幾里得體系的，所以也就與當前的研究沒有關係。- H. S. M. 考克斯特, Regular Polytopes