黃金分割比
元前4世紀建立的比例理論
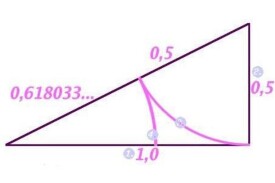
黃金分割比是把一條線段分割為兩部分,使其中一部分與全長之比等於另一部分與這部分之比。由於按此比例設計的造型十分美麗,因此稱為黃金分割比,也稱為中外比。
這個數值的作用不僅僅體現在諸如繪畫、雕塑、音樂、建築等藝術領域,而且在管理、工程設計等方面也有著不可忽視的作用。黃金分割點是指分一線段為兩部分,使得較長的那部分跟原來線段長的比為黃金分割的點。線段上有兩個這樣的點。
這是一個十分有趣的數字,我們以0.618來近似,通過簡單的計算就可以發現:
讓我們首先從一個數列開始,它的前面幾個數是:1、1、2、3、5、8、13、21、34、55、89、144…..這個數列的名字叫做"菲波那契數列",這些數被稱為"菲波那契數"。特點是即除前兩個數(數值為1)之外,每個數都是它前面兩個數之和。
菲波那契數列與黃金分割有什麼關係呢?經研究發現,相鄰兩個菲波那契數的比值是隨序號的增加而逐漸趨於黃金分割比的。即0.618…。由於菲波那契數都是整數,兩個整數相除之商是有理數,所以只是逐漸逼近黃金分割比這個無理數。但是當我們繼續計算出後面更大的菲波那契數時,就會發現相鄰兩數之比確實是非常接近黃金分割比的。
一個很能說明問題的例子是五角星/正五邊形。五角星是非常美麗的,我們的國旗上就有五顆,還有不少國家的國旗也用五角星,這是為什麼?因為在五角星中可以找到的所有線段之間的長度關係都是符合黃金分割比的。正五邊形對角線連滿后出現的所有三角形,都是黃金分割三角形。
由於五角星的頂角是36度,這樣也可以得出黃金分割的數值為2Sin18 。
黃金分割點約等於
是指分一線段為兩部分,使得較長的那部分跟原來線段的長的比為黃金分割的點。線段上有兩個這樣的點。
利用線段上的兩黃金分割點,可作出正五角星,正五邊形。
2000多年前,古希臘雅典學派的第三大算學家歐道克薩斯首先提出黃金分割。所謂黃金分割,指的是把長為L的線段分為兩部分,使其中一部分對於全部之比,等於另一部分對於該部分之比。而計算黃金分割最簡單的方法,是計算斐波契數列1,1,2,3,5,8,13,21,...后二數之比,,,,,...近似值的。
因為它在造型藝術中具有美學價值,在工藝美術和日用品的長寬設計中,採用這一比值能夠引起人們的美感,在實際生活中的應用也非常廣泛,建築物中某些線段的比就科學採用了黃金分割,舞台上的報幕員並不是站在舞台的正中央,而是偏在台上一側,以站在舞台長度的黃金分割點的位置最美觀,聲音傳播的最好。就連植物界也有採用黃金分割的地方,如果從一棵嫩枝的頂端向下看,就會看到葉子是按照黃金分割的規律排列著的。在很多科學實驗中,選取方案常用一種0.618法,即優選法,它可以使我們合理地安排較少的試驗次數找到合理的西方和合適的工藝條件。正因為它在建築、文藝、工農業生產和科學實驗中有著廣泛而重要的應用,所以人們才珍貴地稱它為"黃金分割"。
黃金分割〔Golden Section〕是一種數學上的比例關係。黃金分割具有嚴格的比例性、藝術性、和諧性,蘊藏著豐富的美學價值。應用時一般取0.618 ,就像圓周率在應用時取3.14一樣。
從古希臘至19世紀,甚至到今天,人們一直遵循著一個造型藝術的美學觀——黃金分割,也叫黃金律或中外比。巴托克音樂中對黃金分割法則體現得淋漓盡致,令人驚嘆不己,它集中反映在作品曲式結構與音程法則中。關於巴托克音樂作品中對曲式結構的邏輯性表現為高度的均衡感和適度感,高度的對稱和統一特徵。由此看來,作品內部比例和黃金標界的規律是有著密切的聯繫的,蘭德衛稱這種聯繫不下於維也納古典樂派的方整型樂段在樂曲結構方面的重要性。巴托克的大量作品中,樂曲的高潮恰好在黃金分割點上,即樂曲總長乘以0.618得出的積為樂曲的高潮點。因此,把樂曲可分成長段()與短段(也可理解為)兩大部分,即正方與負方。黃金標界除表現在樂曲總長上外,還可表現在各分段上,長段又可分為兩部分,短段也可分為兩部分,法則與黃金分割法相同。這樣就形成了長段——短段——黃金分割點——短段——長段的對稱圖式,可稱之為“對稱軸”,軸心在黃金時代分割點上。
此處的“軸心”原理與對稱軸在意義上有所不同,它不是以線段長度的數字為依據,而是以音樂情緒發展為依據。此處的數字只是體現了黃金分割在結構造型上的美學意義。
由於公元前6世紀古希臘的畢達哥拉斯學派研究過正五邊形和正十邊形的作圖,因此現代數學家們推斷當時畢達哥拉斯學派已經觸及甚至掌握了黃金分割。
公元前4世紀,古希臘數學家歐多克索斯第一個系統研究了這一問題,並建立起比例理論。
中世紀后,黃金分割被披上神秘的外衣,義大利數家帕喬利稱中末比為神聖比例,並專門為此著書立說。德國天文學家開普勒稱黃金分割為神聖分割。
到19世紀黃金分割這一名稱才逐漸通行。黃金分割數有許多有趣的性質,人類對它的實際應用也很廣泛。最著名的例子是優選學中的黃金分割法或0.618法,是由美國數學家基弗於1953年首先提出的,70年代在中國推廣。
通常用希臘字母 Φ表示這個值。
黃金分割奇妙之處,在於其比例與其倒數是一樣的。例如:1.618的倒數是0.618,而1.618:1與1:0.618是一樣的。
確切值為
黃金分割數是無理數,前面的10位為: 0.6180339887