形心
截面圖形的幾何中心
面的形心就是截面圖形的幾何中心,質心是針對實物體而言的,而形心是針對抽象幾何體而言的,對於密度均勻的實物體,質心和形心重合。
n 維空間中一個對象X的幾何中心或形心是將X分成矩相等的兩部分的所有超平面的交點。非正式地說,它是X中所有點的平均。如果一個物件質量分佈平均,形心便是重心。
如果一個對象具有一致的密度,或者其形狀和密度具有某種對稱性足以確定幾何中心,那麼它的幾何中心和質量中心重合,該條件是充分但不是必要的。
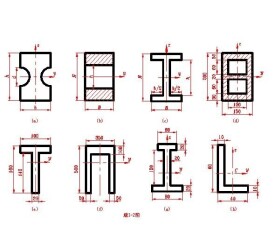
判斷形心的位置:
當截面具有兩個對稱軸時,二者的交點就是該截面的形心。據此,可以很方便的確定圓形、圓環形、正方形。
一個凸對象的幾何中心總在其內部。一個非凸對象的幾何中心可能在外部,比如一個環或碗的幾何中心不在內部。
三角形的重心與三頂點連線,所形成的六個三角形面積相等。
頂點到重心的距離是中線的。
重心、內心、奈格爾點、類似重心四點共線。
三角形的重心同時也是中點三角形的重心。
在直角座標系中,若頂點的座標分別為,則中點的座標為:
三線坐標中、重心的座標為:
形心是三角形的幾何中心,通常也稱為重心,三角形的三條中線(頂點和對邊的中點的連線)交點,此點即為重心。
類似三角形的中心的結論對四面體也成立,四面體的幾何中心是所有頂點和相對平面中心的連線的交點。這些線段被中心分成。這個結論能自然推廣到任何 。如果單形的頂點集是,將這些頂點看成向量,幾何中心位於:
一個由N個頂點確定的不自交閉多邊形的中心能如下計算:
記號與頂點相同。多邊形的面積為:
多邊形的中心由下式給出:
給定有限點集 屬於,它們的中心定義 C為
。
面積中心和質量中心非常類似,面積中心只取決於圖形的幾何形狀。如果物體是均勻的,質量中心將位於面積中心。
對於兩部分組成的圖形,將有如下等式:
是特定部分的面積中心到所選參考系的距離。A是特定部分的面積。
當一個複雜幾何圖形可以分成一些已知的簡單幾何圖形時,先計算各部分的面積中心,然後通過下面一般的公式計算整個圖形的面積中心:
這裡從y-軸到中心的距離是,從x-軸到中心的距離是,中心的坐標是。
圓錐或稜錐的中心位於連接頂點和底的中心的線段上,分比為3:1。
如果中心確定了,那麼中心是所有它對稱群的不動點。從而對稱能全部或部分確定中心,取決於對稱的種類。另外可以知道,如果一個對象具有傳遞對稱性,那麼它的中心是不確定的或不在內部,因為一個傳遞變換群沒有不動點。
地理學中,地球表面一個區域的幾何中心也稱為地理中心。