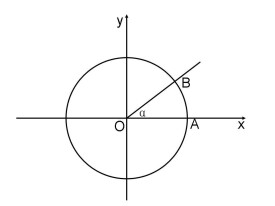
弧長計算公式
一個數學公式
弧長計算公式是一個數學公式,為L=n×π×r/180,L=α×r。其中n是圓心角度數(角度制),r是半徑,L是圓心角弧長,α是圓心角度數(弧度制)。
l=n(圓心角)×π(圓周率)×r(半徑)/180=α(圓心角弧度數)×r(半徑)
在半徑是R的圓中,因為360°的圓心角所對的弧長就等於圓周長C=2πr,所以n°圓心角所對的弧長為l=n°πr÷180°(l=n°x2πr/360°)
例:半徑為1cm,45°的圓心角所對的弧長為
l=nπr/180
=45×π×1/180
=45×3.14×1/180
約等於0.785
扇形的弧長第二公式為:
扇形的弧長,事實上就是圓的其中一段邊長,扇形的角度是360度的幾分之一,那麼扇形的弧長就是這個圓的周長的幾分之一,所以我們可以得出:
扇形的弧長=2πr×角度/360
其中,2πr是圓的周長,角度為該扇形的角度值。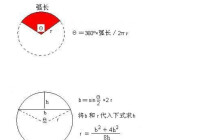

弧長計算公式
扇形面積公式:S(扇形面積)=nπR^2/360
n為圓心角的度數,R為底面圓的半徑
如果已知它的沿圓錐體的一條母線和側面與下底面圓的交線將圓錐體剪開鋪平,就得到圓錐的平面展開圖。它是由一個半徑為圓錐體的母線長,弧長等於圓錐體底面圓的周長的扇形和一個圓組成的,這個扇形又叫圓錐的側面展開圖。
S扇=nπr^2/360
=πrnr/360
=2πrn/360×r/2
=πrn/180×r/2
所以:S扇=rL/2
還可以是S扇=nπr²/360
(n為圓心角的度數,L為該扇形對應的弧長。)
圓錐的表面積=圓錐的側面積+底面圓的面積
其中:圓錐體的側面積=πRL
圓錐體的全面積=πRl+πR²
π為圓周率≈3.14
R為圓錐體底面圓的半徑
L為圓錐的母線長,我們把連接圓錐頂點和底面圓周上任意一點的線段叫作圓錐的母線
(注意:不是圓錐的高)是展開扇形的邊長
n圓錐圓心角=r/l*360 360r/l
側面展開圖的圓心角求法:n=360r/R=πRr或2πr=nπr/180 n=360r/R。如果題目中有切線,經常用的輔助線是連接圓心和切點的半徑,得到直角,再用相關知識解題。
扇形面積
扇形是與圓形有關的一種重要圖形,其面積與圓心角(頂角)、圓半徑相關,圓心角為n°,半徑為r的扇形面積為n/360*πr^2。如果其頂角採用弧度單位,則可簡化為1/2×弧度×半徑。
扇形還與三角形有相似之處,上述簡化的面積公式亦可看成:1/2×弧長×半徑,與三角形面積:1/2×底×高相似。
S扇=(lR)/2(l為扇形弧長)
S扇=(n/360)πR^2(n為圓心角的度數,R為扇形所對應圓的半徑)
S扇=(αR^2)/2(α為圓心角弧度)
註:π為圓周率(3.14159265358979323846264…)
在半徑為R的圓中,n度的圓心角所對應的弧長計算公式為:=