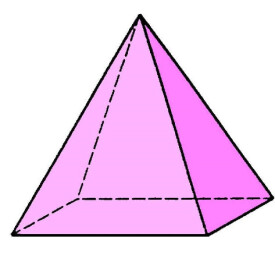
四稜錐
幾何中的立體圖形概念
V=四稜錐的體積
s=四稜錐的底面積
h=四稜錐的高
已知正四稜錐底面邊長為a,側棱長為b,則
正四稜錐底面對角線d為
則正四稜錐的高為
則正四稜錐的體積為
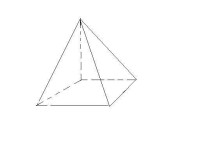
四稜錐
連接之後,發現三稜柱是由三個三稜錐組成,只要證明這三個三稜錐體積相等就可以了。
等底等高,所以體積相等。
換個角度看其實就是等底等高,所以體積相等。所以體積相等。
也就是說組成三稜柱的這三個三稜錐體積相等,所以三稜錐體積是
所以四稜錐的體積計算公式。
四稜錐的底面面積S加頂點A'面積0除以2的平均面積的一個四稜柱乘以高h,就是四稜錐體積: