久期
久期
久期也稱持續期,是1938年由F.R.Macaulay提出的。它是以未來時間發生的現金流,按照目前的收益率折現成現值,再用每筆現值乘以現在距離該筆現金流發生時間點的時間年限,然後進行求和,以這個總和除以債券各期現金流折現之和得到的數值就是久期。概括來說,就是債券各期現金流支付所需時間的加權平均值。金融概念上也可以說是,加權現金流與未加權現金流之比。
久期,全稱麥考利久期-Macaulay duration,數學定義
如果市場利率是Y,現金流(X1,X2,...,Xn)的麥考利久期定義為:D(Y)=[1*X1/(1+Y)^1+2*X2/(1+Y)^2+...+n*Xn/(1+Y)^n]/[X0+x1/(1+Y)^1+X2/(1+Y)^2+...+Xn/(1+Y)^n]
即 D=(1*PVx1+...n*PVxn)/PVx
其中,PVXi表示第i期現金流的現值,D表示久期。
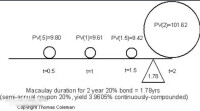
Macaulay Duration Example
例子:假設有一債券,在未來n年的現金流為(X1,X2,...Xn),其中Xi表示第i期的現金流。假設利率為Y0,投資者持有現金流不久,利率立即發生升高,變為Y,問:應該持有多長時間,才能使得其到期的價值不低於利率為Y0的價值?
通過下面定理可以快速解答上面問題。
定理:PV(Y0)*(1+Y0)^q<=PV(Y)(1+Y)^q的必要條件是q=D(Y0)。這裡D(Y0)=(X1/(1+Y0)+2*X2/(1+Y0)^2+...+n*Xn/(1+Y0)^n)/PV(Y0)
q即為所求時間,即為久期。
上述定理的證明可通過對Y導數求倒數,使其在Y=Y0取局部最小值得到。
久期是債券平均有效期的一個測度,它被定義為到每一債券距離到期的時間的加權平均值,其權重與支付的現值成比例。
久期是考慮了債券現金流現值的因素后測算的債券實際到期日。價格與收益率之間是一個非線性關係。但是在價格變動不大時,這個非線性關係可以近似地看成一個線性關係。也就是說,價格與收益率的變化幅度是成反比的。值得注意的是,對於不同的債券,在不同的日期,這個反比的比率是不相同的。
在債券分析中,久期已經超越了時間的概念。修正久期大的債券,利率上升所引起價格下降幅度就越大,而利率下降所引起的債券價格上升幅度也越大。可見,同等要素條件下,修正久期小的債券比修正久期大的債券抗利率上升風險能力強;但相應地,在利率下降同等程度的條件下,獲取收益的能力較弱。
正是久期的上述特徵給我們的債券投資提供了參照。當我們判斷當前的利率水平存在上升可能,就可以集中投資於短期品種、縮短債券久期;而當我們判斷當前的利率水平有可能下降,則拉長債券久期、加大長期債券的投資,這就可以幫助我們在債市的上漲中獲得更高的溢價。
久期的應用
久期是一種測度債券發生現金流的平均期限的方法。由於債券價格敏感性會隨著到期時間的增長而增加,久期也可用來測度債券對利率變化的敏感性,根據債券的每次息票利息或本金支付時間的加權平均來計算久期。
久期的計算就當是在算加權平均數。其中變數是時間,權數是每一期的現金流量,價格就相當於是權數的總和(因為價格是用現金流貼現算出來的)。這樣一來,久期的計算公式就是一個加權平均數的公式了,因此,它可以被看成是收回成本的平均時間。
決定久期即影響債券價格對市場利率變化的敏感性包括三要素:到期時間、息票利率和到期收益率。
不同債券價格對市場利率變動的敏感性不一樣。債券久期是衡量這種敏感性最重要和最主要的標準。久期等於利率變動一個單位所引起的價格變動。如市場利率變動1%,債券的價格變動3%,則久期是3。
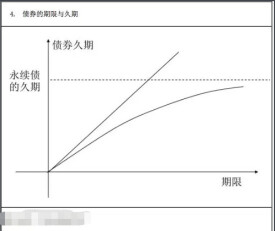
定理一:只有零息債券的馬考勒久期等於它們的到期時間。
定理二:直接債券的馬考勒久期小於或等於它們的到期時間。
定理三:統一公債的馬考勒久期等於(1+1/y),其中y是計算現值採用的貼現率。
定理四:在到期時間相同的條件下,息票率越高,久期越短。
定理五:在息票率不變的條件下,到期時間越久,久期一般也越長。
定理六:在其他條件不變的情況下,債券的到期收益率越低,久期越長。
債券(bond)是發行人根據債券發行時規定的規則向債券持有人支付貨幣的一種義務。一般來說,一張債券支付一筆具體的數額,即它的面值(face value),或者是它在到期日的平價(par value)。
債券的票面因素包括以下幾個:①債券的票麵價值即面值,是債券票面表明的貨幣價值,是債券發行人承諾在債券到期日償還給債券持有人的金額。②債券的到期期限,是指債券從發行之日起到償清本息之日止的時間,也是債券發行人承諾履行合同義務的全部時間。③債券的票面利率,亦即票息率,是債券年利息和票麵價值得比率。實際中債券利率有多種形式,比如單利、複利、貼現利率等。④債券的發行者名稱。這是為了明確債券的債務體,也是為債權人到期時追索本息提供依據。
債券的前三個票面因素再加上實際收益率,就提供了確定債券價格的基本要素。以一個票息率固定,期間定期支付票息,最後票息和本金一起支付的固定收益債券為例,來分析它的現金流。定義c為票息率,F為票麵價值,到期前有Ct=Fc,到期時則有CT=cF+F,當收益率為y時,該債券的現值可以表達為下式:
其中:
— 第t個時期的現金流
— 最後到期時的時期數
— 每次支付的時期數
—收益率
當債券的發行價格等於P時稱為平價發行,大於P時稱為溢價發行,低於P時稱為折價發行。

久期分析
其中,和 分別為 關於的一階和二階導數。這個表達式為計算債券價格隨收益率的波動情況的變化提供了很好的方法。如果只是做最基本的估計,就可以只考慮前兩項,而把第三項忽略不計。這樣,關於y的一階導數就非常重要了,而這個一階導數即為F.R.Macaulay在1938年提出的概念:久期(duration)。
這個D也稱為“Macaulay久期”,它一方面代表著債券的實際到期時間,另一方面又是債券價格對於利率變動的靈敏性度量。
實際上,久期在數值上和債券的剩餘期限近似,但又有別於債券的剩餘期限。在債券投資里,久期被用來衡量債券或者債券組合的利率風險,它對投資者有效把握投資節奏有很大的幫助。
一般來說,久期和債券的到期收益率成反 比,和債券的剩餘年限成正比,和票面利率成反比。一個特殊的情況是,當一個債券是貼現發行的無票面利率債券,那麼該債券的剩餘年限就是其久期。這也是為什麼人們常常把久期和債券的剩餘年限相提並論的原因。
從上面的討論中可知:對於給定的到期收益率的微小變動,債券價格的相對變動與其 Macaulay久期成比例。當然,這種比例關係只是一種近似的比例關係,它的成立是以債券的到期收益率很小為前提的。為了更精確地描述債券價格對於到期收益率變動的靈敏性,又引入了修正久期模型(Modified Duration Model)。修正久期被定義為:△P/P=-(D*)dy+C[(dy)^2]/2
從這個式子可以看出,對於給定的到期收益率的微小變動,債券價格的相對變動與修正久期之間存在著嚴格的比例關係。所以說修正久期是在考慮了收益率項 y 的基礎上對 Macaulay 久期進行的修正,是債券價格對於利率變動靈敏性的更加精確的度量。
淺顯易懂的解釋:修正久期就是債券價格相對於利率水平正常變動的敏感度。如果一隻短期債券基金的投資組合修正久期是2.0,那麼利率每變化1個百分點,該基金價格將上升或下降2%;一隻長期債券型基金的投資組合修正久期是12.0,那麼利率每變化1個百分點,其價格將上升或下降12%。
在Macaulay久期模型研究中存在一個重要假設,即隨著利率的波動,債券的現金流不會發生變化。然而這一假設對於具有隱含期權的金融工具,如按揭貸款、可贖回(或可賣出)債券等而言則很難成立。因此,Macaulay久期模型不應被用來衡量現金流易受到利率變動影響的金融工具的利率風險。針對Macaulay久期模型這一局限,FrankFabozzi提出了有效久期的思想。所謂有效久期是指在利率水平發生特定變化的情況下債券價格變動的百分比。它直接運用不同收益率變動為基礎的債券價格進行計算,這些價格反映了隱含期權價值的變動。其計算公式為:
Duration(effective) = (V-Δy - V+Δy) ÷ 2V0Δy
其中:
V-Δy 利率下降x個基點時債券價格;
V+Δy 利率上升x個基點時債券價格;
-Δy 初始收益率加上x個基點;
+Δy 初始收益率減去x個基點;
V0 債券初始價格;
有效久期不需要考慮各期現金流的變化情況,不包含利率變化導致現金流發生變化的具體時間,而只考慮利率一定變化下的價格總體情況。因此,有效久期能夠較準確地衡量具有隱含期權性質的金融工具的利率風險。對於沒有隱含期權的金融工具,有效久期與Macaulay久期是相等的。
隨著對久期模型研究的不斷深入,相繼有人提出了方向久期、偏久期、關鍵利率久期、近似久期以及風險調整久期等新的久期模型,把利率的期限結構、票息率的改變以及信用風險、贖回條款等加入到模型裡面,使久期模型得到了進一步的發展。
債券組合久期
債券投資組合也有相應的久期概念,其久期為單個久期的加權平均,可以用下面的公式進行計算:
其中為單個債券在組合中的權重。
利用久期控制利率風險
在債券投資里,久期可以被用來衡量債券或者債券組合的利率風險,一般來說,久期和債券的到期收益率成反比,和債券的剩餘年限及票面利率成正比。對於一個普通的附息債券,如果債券的票面利率和其當前的收益率相當的話,該債券的久期就等於其剩餘年限當一個債券是貼現發行的無票面利率債券,那麼該債券的剩餘年限就是其久期。債券的久期越大,利率的變化對該債券價格的影響也越大,因此風險也越大。在降息時,久期大的債券上升幅度較大;在升息時,久期大的債券下跌的幅度也較大。因此,預期未來升息時,可選擇久期小的債券。在債券分析中久期已經超越了時間的概念,投資者更多地把它用來衡量債券價格變動對利率變化的敏感度,並且經過一定的修正,以使其能精確地量化利率變動給債券價格造成的影響。修正久期越大,債券價格對收益率的變動就越敏感,收益率上升所引起的債券價格下降幅度就越大,而收益率下降所引起的債券價格上升幅度也越大。
債券對利率變動的反應特徵如下:債券價格與利率變化反向變動;在給定利率變化水平下,長期債券價格變動較大,因此債券價格變化直接與期限有關;隨著到期時間的增加,債券對於利率變化的敏感度是以一個遞減的速度增長;由相同幅度的到期收益率的絕對變化帶來的價格變化是非對稱的,具體來說,在期限給定條件下,到期收益率降低引起的價格上升,大於到期收益率上升引相同幅度起的價格下降;票息高的債券比那些票息低的債券對利率的敏感性要低。
利用久期進行免疫
所謂免疫,就是構建這樣的一個投資組合,在組合內部,利率變化對債券價格的影響可以互相抵消,因此組合在整體上對利率不具有敏感性。而構建這樣組合的基本方法就是通過久期的匹配,使附息債券可以精確地近似於一隻零息債券。利用久期進行免疫是一種消極的投資策略,組合管理者並不是通過利率預測去追求超額報酬,而只是通過組合的構建,在迴避利率波動風險的條件下實現既定的收益率目標。在組合品種的設計中,除了國債可以選入組合外,部分收益率較高的企業債券及金融債券也能加入投資組合,條件是控制好匹配的久期。
但是,免疫策略本身帶有一定的假設條件,比如收益率曲線的變動不是很大,到期收益率的高低與市場利率的變化之間有一個平衡點,一旦收益率確實發生了很大的變動,則投資組合不再具有免疫作用,需要進行再免疫,或是再平衡;其次,免疫嚴格限定了到期支付日,對於那些支付或終止期不能確定的投資項目而言並不是最優;再次,投資組合的免疫作用僅對於即期利率的平行移動有效,對於其他變動,需要進一步拓展應用。
利用久期優化投資組合
進行免疫后的投資組合,雖然降低了利率波動的風險,但是組合的收益率卻會偏低。為了實現在免疫的同時也能增加投資的收益率,可以使用回購放大的辦法,來改變某一個債券的久期,然後修改免疫方程式,找到新的免疫組合比例,這樣就可以提高組合的收益率。但是,在回購放大操作的同時,投資風險也在同步放大,因此要嚴格控制放大操作的比例。
本文在債券價格基礎上,進行了久期的公式推導,分析了久期在債券投資中的重要作用。但是久期只是債券價格關於收益率的一階導數,單獨使用久期近似估計債券價格隨收益率的波動情況,不是十分準確。因此價格關於收益率的二階導數,即凸性(convexity),在債券投資中也是十分重要的工具,它經常和久期配合使用,提高預測的精度。近些年來,久期模型逐漸考慮了信用風險、利率風險、稅收風險等各種風險因素,使久期模型得到了更大的發展。但是如何把這些最新的模型應用於債券投資的實踐,還需要做很多的工作。