共找到2條詞條名為解集的結果 展開
- 方程解的集合
- 山東省德州市慶雲縣解集城西的村莊
解集
方程解的集合
解集是一個數學用語,指以一個方程(組)或不等式(組)的所有解為元素的集合叫做該方程(組)或不等式(組)的解集。表示解的集合的方法有三種:列舉法、描述法和圖示法。解集作為數學中的重要工具,在數學中有著十分廣泛的應用。
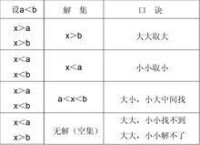
尋找解集的方法
例:
集;
的解集就是;
的解集是。
方程(組)或不等式(組)的所有解均在其解集中,解集中的所有元素均為方程(組)或不等式(組)的解。無解的方程(組)或不等式(組)的解集為空集。
線性代數里向量(或矩陣)方程的解集是向量(或矩陣),這類元素構成集合,就不能稱為區間或區域了。
對於二元不等式(組)的解集就是一個平面區域。
解集的表示法也即集合的表示法,就是給出一個集合和組成這個集合的元素的表示方法。表示集合的方法有三種。
列舉法,又叫外延法。把集合的元素一一列舉出來,寫在大括弧“{}”內,並用逗號“,”把它們彼此分開。例如,小於10的素數集合A可表示為。又如3的自然數冪所組成的集合B可表示為。在用列舉法表示一個無限集或元素很多的集的時候常用省略號。這時,要注意表示的明確性,要能從已經列舉的元素中知道被省略的元素是什麼。在用列舉法表示集合時,元素的次序無關緊要,但不允許重複。
描述法,又稱特徵性質法或內涵法。利用概括原則指出確定集合元素的特徵性質P(x),從而給出集合的方法稱為描述法。具有性質P(x)的所有元素x組成的集合A記為或。其中表示集合中元素的特徵性質。所謂集合元素的特徵性質是指:集合的每個元素的共有的性質,並且不屬於這個集合的元素都不具有這個性質。
圖示法
圖示法,如維恩圖法。用圓、橢圓、矩形或其他封閉曲線圍成的區域表示集合。如圖1所示,矩形表示全集I,曲線包圍的區域表示集合A,B,C等。這種方法嚴格地說應稱示意法,有一定的局限性,但它的直觀性能幫助人們思考。