樣本協方差矩陣
多元分析的基本概念之一
樣本協方差矩陣
樣本協方差矩陣
樣本協方差矩陣
通常,我們將 數據矩陣記為 或,第i行第j列對應的元素可表示為,我們將矩陣表示為。的行可以表示為
或者
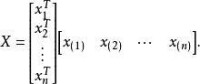
樣本協方差矩陣
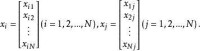
樣本協方差矩陣
第i個變數的樣本方差是
第i個變數和j個變數之間的樣本協方差為
向量 的均值為
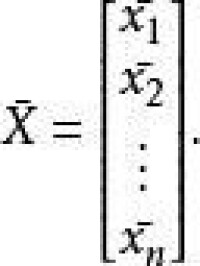
樣本協方差矩陣
稱為樣本協方差矩陣,或簡稱為“協方差矩陣”。使用矩陣符號來表示統計量更為簡便。
記
樣本協方差矩陣
其中,稱為中心矩陣,我們得到如下標準形式
這是樣本協方差矩陣的一種簡便矩陣表達式。我們總計需要nN個樣本點來估計樣本協方差矩陣S。轉向表格,我們可以將nN個樣本點的信息“歸納”到單一矩陣S中。在頻譜感知中,我們會得到某些隨機變數的長記錄數據或大數據維度的一個隨機向量。
在多元分析中,樣本協方差矩陣的研究是基礎。擁有現代數據,矩陣往往非常大,變數數目與樣本量相當(即所謂的“大數據”)。在這種環境中,最大特徵值或主成分方差的分佈往往鮮為人知。在數學物理和概率域,隨機矩陣理論的一·個驚喜是:對於相對較小的n和p來說.這些結果似乎能夠提供與主成分有關的有用信息。
樣本協方差矩陣
樣本協方差矩陣
樣本協方差矩陣
假定X是一個p×n數據矩陣。人們通常考慮p維列向量(其協方差矩陣為 )的n個觀測值或情形。為明確起見,我們假定行 服從獨立高斯分佈。特別是,平均值已被減去:如果我們也不用擔心被n除,則我們將 稱為樣本協方差矩陣。在高斯假設下,我們稱“符合Wishart分佈。如果=1,則屬於“空”情形,我們稱其為白色Wishart,類似於時間序列設置,在該設置中,白色頻譜在所有頻率處具有相同的方差。
多元分析中的大樣本工作歷來假定n/p(每個變數對應的觀測值數)取值較大。如今,p取大值甚至巨值都是常見的,因而n/p取值範圍為從中到小。在極端情況下,甚至小於1。
樣本協方差矩陣的特徵值和特徵向量分解過程可表示為
一個基本的現象是,相同的特徵值z;要比特徵值A。應用範圍更廣。在空的情形中,當所有總體特徵值相同時,這一效果最為明顯。
