共找到2條詞條名為布拉格方程的結果 展開
- 1913年提出的物理學概念
- 布拉格定律
布拉格方程
1913年提出的物理學概念
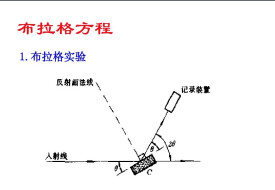
布拉格方程:對於X射線衍射,當光程差等於波長的整數倍時,晶面的散射線將加強,此時滿足的條件為2dsinθ=nλ,其中,d為晶面間距,θ為入射線,反射線與反射晶面之間的夾角,λ為波長,n為反射級數,布拉格方程是X射線在晶體產生衍射時的必要條件而非充分條件。有些情況下晶體雖然滿足布拉格方程,但不一定出現衍射,即所謂系統消光。
布拉格方程是給出晶體X射線衍射方向的方程。
d為晶面間距,θ為入射束與反射面的夾角,λ為X射線的波長,n為衍射級數,其含義是:只有照射到相鄰兩鏡面的光程差是X射線波長的n倍時才產生衍射。
該方程是晶體衍射的理論基礎。
設一單色波(任何種類),進入一組對齊的平面晶格點,其平面間距為d,入射角為,如圖1所示。波被晶格點A反射後會沿AC'行進,而沒有被反射的波則沿AB繼續行進,被晶格點B反射後路徑為BC。AC'與BC間存在路徑差,表達式為
只有在路徑差等於波長的整數倍時,這兩股分開的波,在到達某一點時,會是同相位的,才會因此產生相長干涉,故相長干涉的產生條件為, (需要為C'下定義)
其中 n與的定義同上。
從圖1可見,且,
由此可得,
組合上述各式,得
簡化后可得:
即布拉格方程。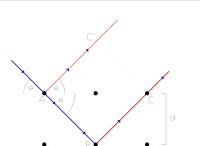

布拉格方程
膠體晶體為一種非常有序的粒子陣列,可以在大範圍內形成(長度從幾微米到幾毫米不等),而且可被看作原子及分子晶體的類比。球狀粒子的周期性陣列,會形成出相似的空隙陣列,而這種陣列可被用作可見光的衍射光柵,尤其是當空隙與入射波長為同一數量級的時候。
因此,科學家們在很多年前就發現了,由於相斥庫侖相互作用的關係,水溶液中的帶電荷高分子,會表現出大範圍的類晶體相互關聯,當中粒子間距一般會比粒子直徑要大得多。在自然的所有這種例子中,都可到看到一樣的漂亮構造色(或晃動的色彩),這都可以歸功於可見光波的相長干涉,而此時光波會滿足布拉格條件,跟結晶固體的X射線衍射類似。
該方程是晶體衍射的理論基礎。是衍射分析中最重要的基礎公式,它簡單明確地闡明衍射的基本關係,應用非常廣泛。歸結起來,從實驗上可有兩方面的應用:
一、用已知波長的X射線去照射未知結構的晶體,通過衍射角的測量求得晶體中各晶面的間距d,從而揭示晶體的結構,這就是結構分析(衍射分析);
二、用已知晶面間距的晶體來反射從樣品發射出來的X射線,通過衍射角的測量求得X射線的波長,這就是X射線光譜學。該法除可進行光譜結構的研究外,從X射線波長尚可確定試樣的組成元素。電子探針就是按照這一原理設計的。
● 晶格
● 衍射
● 分散式布拉格反射器
● 光纖布拉格光柵
● 亨德森極限
● 衍射的動力學理論
● 勞厄方程
● 粉末衍射
● 結構因子
● X射線晶體學