對角線
幾何學名詞
對角線,幾何學名詞,定義為連接多邊形任意兩個不相鄰頂點的線段,或者連接多面體任意兩個不在同一面上的頂點的線段。另外在代數學中,n階行列式,從左上至右下的數歸為主對角線,從左下至右上的數歸為副對角線。
“對角線”一詞來源於古希臘語“角”與“角”之間的關係,後來被拉入拉丁語(“斜線”)。
連接多邊形任意兩個不相鄰頂點的線段,或者連接多面體任意兩個不在同一面上的頂點的線段.
從n邊形的一個頂點出發,可以引條對角線
n邊形共有個對角線
◎關於矩形對角線的知識:
長×長+寬×寬=對角線×對角線(其實就是勾股定理)即兩個直角邊的平方和等於斜邊的平方。
狹義的對角線,是在多邊形中任意兩個非鄰接的頂點的連線(線段).
廣義的對角線,是在多維度體中任意兩個非鄰接的頂點的連線(線段).
在n階行列式中,從左上至右下的數歸為主對角線,從左下至右上的數歸為副對角線。
克萊姆(Cramer)法則:主對角線的數分別相乘,所得值相加;副對角線的數分別相乘,所得值的相反數相加。兩者總和為行列式的值。此法僅適用於小於4階的行列式。(如右圖)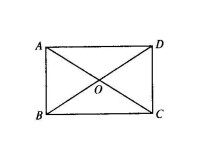

對角線
一個階矩陣的對角線為所有第k行第k列元素的全體,
設X,Y是任意兩個集合,按定義一切序對所構成的集合:
叫做集合X,Y(按順序)的直積或笛卡爾積,叫做。
集合中的對角線:
是的一個子集,它給出集X中元素的相等關係,事實上,a△b表示。即。
一.利用對角線判定特殊的四邊形
在課堂上我們已探索過以下幾個重要的結論:
⑴對角線互相平分的四邊形是平行四邊形;
⑵對角線互相平分且相等的四邊形是矩形;
⑶對角線互相平分且垂直的四邊形是菱形;
⑷對角線相等且互相垂直平分的四邊形是正方形;
⑸對角線相等的梯形是等腰梯形。
其實以上這些結論是有聯繫的。如圖1,四邊形ABCD中,兩條對角線相交於點O。
⑴當OA=OC,OB=OD時,四邊形ABCD是平行四邊形。
⑵在OA=OC,OB=OD的基礎上增加AC=BD條件時,四邊形ABCD在平行四邊形的基礎上變成矩形。
⑶在OA=OC,OB=OD的基礎上增加AC⊥BD條件時,四邊形ABCD在平行四邊形的基礎上變成菱形。
⑷在OA=OC,OB=OD的基礎上增加AC=BD,AC⊥BD條件時,四邊形ABCD在平行四邊形的基礎上變成正方形。
⑸當AB//CD,且,OA=OB時,此時的四邊形ABCD為對角線相等的梯形,即等腰梯形。
由此可知,把一個一般的四邊形變為特殊的四邊形,可以通過改變兩條對角線的大小關係和位置關係來完成。這也是特殊四邊形之間重要的聯繫紐帶之一。
二.利用對角線判定動態四邊形的形狀
如圖2,中,點O是邊AC上的一個動點,P是BC延長線上一點。過點O作直線,設MN交∠BCA的平分線於點E,交∠PCA的平分線於點F,連結AE、AF。
⑴圖中有等腰三角形嗎?
⑵當點O運動到何處時,四邊形AECF是矩形?簡要說明理由。
⑶在⑵中的矩形可能是正方形嗎?此時應滿足什麼條件?
分析:⑴圖2中有等腰三角形。
理由:
是等腰三角形。
⑵當點O運動到AC的中點時,四邊形AECF是矩形。理由如下:
由⑴得。
由O是AC的中點,得。
所以:
所以四邊形AECF的兩條對角線AC、EF互相平分且相等。故四邊形AECF為矩形。
所以,當點O運動到AC的中點時,四邊形AECF是矩形。
⑶在⑵中的矩形可能是正方形。
理由:因為,當時,,即對角線AC、EF互相垂直。
所以這時四邊形AECF是正方形。
即在這當中,當時,在⑵中的矩形AECF是正方形。
1、在工程中,對角支架是用於支撐矩形結構(例如腳手架)的梁以承受推入其中的強力;雖然被稱為對角線,但由於實際考慮,對角線通常不連接到矩形的角部。
2、對角線鉗是指刀口切割邊緣所定義的鋼絲鉗,它與關節鉚釘相交於一個角度或成“對角線”,因此得名。
3、對角線捆綁是用於將翼梁或桿結合在一起的綁紮類型,使得綁帶以一定角度交叉在桿上。
4、在英式足球中,對角線控制戰術是裁判和助理裁判將自己定位在球場四個象限中的一個位置。