極限序數
極限序數
極限序數(limit ordinal number)集合論術語,是指一類特殊的序數。指不為0且不是後繼序數的序數。
集合論是德國數學家康托兒於19世紀末創立的,以集合為研究對象的一個數學基本分支。集合論的內容幾乎滲透到數學的一切領域,它在現代數學的發展中起了很大的作用,是現代數學各個分支的基礎。按照現代數學的觀點,數學各個分支都可以看作是研究具有某種特定結構的集合。
極限序數(limit ordinal number)是一種序數。若α≠0且α不是後繼序數,則稱α為極限序數。極限序數不直接跟在某個序數之後,因此它有這樣的性質:若β<α,則必有序數γ滿足β<γ<α。因而極限序數α又滿足:
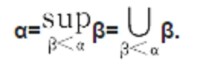
極限序數
極限序數是一類特殊的序數。指不為0且不是後繼序數的序數。一切序數被分成三類:
1.只含0這個序數。
2.後繼序數。
3.極限序數。
ω={0,1,2,…}是最小的極限序數。序數可按順序列出如下:
0,1,2,…,
ω,ω+1,ω+2,…,
ω·2,ω·2+1,…,ω·3,…,ω·4,…,
ω·ω=ω,ω+1,…,ω+ω,…,
ω·2,…,ω,…, ω,…,ω,
ω+1,…,ω·2,…,
ω·ω=ω,…,ω,…,ω,…,ω,…,ω,…,
其中ω,ω·2,ω·3,ω,ω,ω等都是極限序數。
集合論的基本概念之一,是日常使用的第一、第二……表示次序的數的推廣。序數概念是建立在良序集概念之上的。序數原來被康托爾(Cantor,G.F.P.)定義為良序集的序型,而良序集A的序型A-,作為從A的結構屬性抽象出來的結果,是所有與集A同構的一切良序集的共同特徵,即A-={B|BA}。這一定義從形式上看簡單明了,但可惜這樣的不是ZFC系統中的集合。事實上{B|BA}是一個真類。
1923年和1928年,馮·諾伊曼(von Neumann,J.)為了克服上述定義的缺陷,把序數定義為滿足下述條件的良序集α:對於一切ξ∈α,S(ξ)=ξ.這裡S(ξ)={β∈α|β<ξ}稱為良序集α中由ξ生成的初始段。例如,在集合9={0,1,…,8}中任取一元素x,則S(x)={0,1,…,x-1},所以9是一序數。集A稱為歸納集,如果:
1.∅∈A.
2.只要a∈A,就有a′=a∪{a}∈A.
A的一切歸納子集之交N是自然數集。它是最小的歸納集。N是良序的,且對任何n∈N都有:
S(n)={0,1,…,(n-1)}=n,
所以N是序數,記為ω。自然數集N的每個元素n都是序數,稱為有限序數。其他序數稱為超窮序數。ω是最小的超窮序數.
1937年,魯賓孫(Robinson,R.M.)給出序數的另一等價定義:良序集〈α,∈〉是一個序數,若〈α,∈〉是傳遞集,即只要x∈α且y∈x就有y∈α。
序數也可用遞歸的方法來定義:
1.0是序數。
2.若α是序數,則α′=α∪{α}是序數。
3.若S是序數的集合,則∪S是序數。
4.任一序數都由上述1—3得到。
后三種定義沒有康托爾原定義的缺點。序數有三種,第一種是0;第二種是後繼序數α′=α∪{α};其他序數屬第三種,稱為極限序數。對任何良序集A,有且僅有一個序數α使A與α同構,此時α稱為A的序數,用A-=α表示。
任何兩個具有相同序數的良序集必定序同構,因此,序數是同構的良序集的共同特徵。這正是康托爾序數概念的實質。對任何序數α和β,定義α<β,當且僅當α∈β。
序數有下列性質:設α,β和γ是序數。
1.若α<β,β<γ,則α<γ。
2.α<β和β<α不能同時成立。
3.α<β或α=β或β<α之一成立。
4.每個非空的序數集合有一個關於<的最小元,因此每個序數集都可用關係<將它良序化。
5.每個序數集合X,都存在序數α,使得α∉ X。
一類特殊的序數。如果序數α是某個序數的後繼,則稱α為後繼序數,即存在序數β,使得α=S(β)=β∪{β}。非0且非後繼的序數稱為極限序數。非0的自然數都是後繼序數。例如:
1=0∪{0}=S(0);
2=1∪{1}=S(1);
…
同樣,ω+1,ω+2,…也是後繼序數。但0, ω,ω等則不是後繼序數。