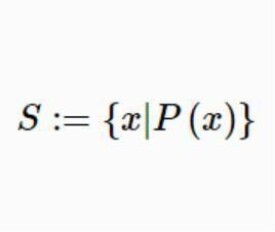概括原則
概括原則
概括原則(principle of comprehension)是古典集合論的基本原則，指古典集合論中用以構造集合的一個重要規定或公理，其內容為無條件承認任給一個性質P，人們就能把所有滿足該性質P的對象，且僅由這些具有性質P的對象彙集在一起而構成一個集合。用符號來表示就是G=x|P(x)，其中“|”左邊的x表示集合G的任一元素，而“|”右邊的P(x)表示元素x具有性質P，表示把所有具有性質P的x彙集在一起而構成一集合。因此，概括原則的另一表達式為ᗄx(x∈A↔P(x))，亦即凡是集A之元素必具有性質P，反之，凡具有性質P的對象必為集A之元素。所以，概括原則是一條集合存在性公理(公理模式)。在德國數學家康托爾(Cantor，G.(F.P.))的早期工作中，概括原則只是隱蔽地被使用著，後來德國數學家、數理邏輯學家弗雷格(Frege，(F.L.)G.)公開地採用這一公理模式。對於概括原則內容的理解和使用，還應特別指出如下幾點：1.概括原則中用以造集的那個性質P必須是精確性一元謂詞，任何非精確性一元謂詞都不是康托爾意義下用以造集的謂詞，這個大前提無論是康托爾還是弗雷格都沒有明文敘述，只是在使用概括原則時無形地貫徹。2.在概括原則之下用以造集的精確性一元謂詞是完全任意的，而且對象域也是沒有任何限制的。3.給定精確性一元謂詞后，由概括原則所構造之集惟一確定，它恰由所有滿足該謂詞的對象組成。
概括原則是集合論的一項重要原則，是集合論創始人康托爾(G.F.P.Cantor)提出的確定集合的基本原則：對於任何性質P，都存在一個集合A，它恰好由具有性質P的所有元素組成，即。康托爾提出的這一確定集合的原則失之過寬(例如，由它允許x是自己的元素這個性質出發，會導出一些悖論(如著名的羅素悖論)，而被認為是不正確的。分離公理彌補了概括原則的缺點(參見“分離公理”)，把集合限制為由已給集合與已給性質共同確定的對象。例如，它不允許一切集合的集合存在。用概括原則確定的對象稱為類。任何性質P都確定一個類。類可以是集合，可以不是集合，不是集合的類稱為真類，例如，完全類就是真類，而空類就是集合：空集∅，對於類仍可如下定義包含關係與各種運算：
1.；
2.；
3.；
4.；
5. 。
為了給出一個集合，常常是列舉出該集合的元素，這種方法的好處是具有明顯性，比如，令集合，我們一眼就看出它只有三個元素，即0，1，4，但是，在有些情況下，這樣做是很不方便的，比如令集合為：
式(1)所確定的集合就有點煩瑣了，這樣大的數目再多列出幾個，那就更複雜甚至無法寫出。
當我們分析一下的元素的性質時，就會發現這些數都是有規律的，它們是18到24之間的這七個自然數的立方數，亦即當x滿足時，的元素恰為 ，這樣就有：
其中豎杠的前邊是集合的元素，它必須滿足豎杠的後邊所列舉的條件，亦即“x是一自然數且並且，這個條件也叫做一個性質。(2)表明的元素都具有性質為“把這個元素開立方，立方根為18與24(包括18和24在內)之間的自然數”.不難驗證它的元素恰好是在(1)中所列舉的那些．由外延原則，(1)與(2)定義了同樣的集合。
當我們把(2)式中的條件改為“x是一自然數且並且時，所定義的集合稱為，如果要用類似於(1)式那樣的顯式去列舉時，那將是很煩瑣的事情了。如果把(2)式中的條件改為：“x是一有理數且且”時，這時如果要使用(1)那樣的顯式，枚舉這樣的集合的全部元素就幾乎不可能。為此，為了方便、簡潔地給出一個集合，就需採用如像(2)這樣的定義方式，上述所列舉的條件都叫做性質，康托爾把所有滿足給定性質的元素彙集在一起而成為一個集合，並且稱之為 概括原則。也就是說：
概括原則 任給一個性質P，那麼存在著一個集合S，它的元素恰好是具有性質P的那樣的一些對象，亦即
其P(x)是“x具有性質P”的一個縮寫。這樣，就有。
這條原則在使用上是強有力的，而且也是很方便的。比如，集合{2，3，4，8}，可用條件“或者或者或者”來給出，可記成：
．
在下邊，我們用“∨”表示“或者”，用“∧”表示“並且”。
例如：；
就是集合N；
就是集合。
應該指出，使用概括原則要有限制，否則會出毛病。
對於任意性質P(x)，都存在一個類(包括集合)C，使，其中，P(x)是描述任意對象之屬性的謂詞，它表示x具有性質P。其形式化表示為
註釋 對任意屬性謂詞P(x)，都可決定一個類，且滿足：
x屬於C 當且僅當 x滿足P(x)
當用P(x)能夠解釋一個集合C時，也稱P(x)為集合C的入集條件。
設x是任意對象，是一個對x的屬性描述。按照概括原則，可用P(x)去規定一個類T，，這時，由於T也是對象。故與不能同時成立，也不能同時不成立。
如果成立，即T滿足P(x)，這時，按照概括原則有，從而引出了矛盾。
如果成立，這時T是T的元素，那麼按照概括原則T滿足P(x)，即。
顯然，由這個P(x)所規定的不是集合。
羅素的證明，拯救了數學基礎理論所面臨的一場災難。弗雷格(Frege)在他的《算術的基本法則》第二卷即將付印之時，收到羅素先生的一封信，羅素將集合論的悖論告訴了他。弗雷格在他書的尾頁上寫道：“一個科學家不會碰到比這更難堪的事了。即在工作完成之際，它的基礎垮了。”
羅素指出概括原則規定的是類，在這些類中有一些是真類，正如。它們不是集合。子集分離原則對概括原則作了補充，使集合悖論得以消除。
基本信息
- 中文名
- 概括原則
- 外文名
- principle of comprehension
- 別名
- 概括公理
- 提出者
- 康托爾(G.F.P.Cantor)
- 所屬學科
- 數學（集合論）
- 簡介
- 古典集合論的基本原則