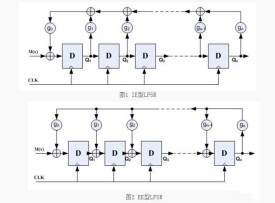
反饋移位寄存器
反饋移位寄存器
ai表示二值(0,1)存儲單元,ai的個數n稱為反饋移位寄存器的級。在某一時刻,這些級構成該反饋移位寄存器的一個狀態,共有2^n個可能狀態,每一個狀態對應於域GF(2)上的一個n維向量,用(a1,a2,a3,…an)表示。在主時鐘周期的周期區間上,每一級存儲器ai都將內容向下一級ai-1傳遞,並根據寄存器的當前狀態f(a1,a2,a3,…an)作為an的下一時間內容,即從一個狀態轉移到下一個狀態。其中函數f(a1,a2,a3,…an)稱為該反饋移位寄存器的反饋函數。
: linear feedback shift register simu-lated (簡稱: LFSR)
線性和非線性反饋移位寄存器
如果反饋函數f(a,a,a,…a)是a,a,a,…a 的線性函數函數,則該反饋移位寄存器是線性反饋移位寄存器,用LFSR表示,比如:f(a,a,a,…a)=ka⊕ka⊕….⊕ka⊕ka,其中係數k∈{0,1}(i=1,2,3,…,n)。
相應的如果反饋函數f(a,a,a,…a)是a,a,a,…a 的非線性函數函數,則該反饋移位寄存器是非線性反饋移位寄存器。
移位寄存器序列
反饋函數f(a,a,a,…a)為n元布爾函數。在時鐘脈衝時,如果反饋移位寄存器的狀態為s=(a,…..a)則
a=f(a,a,...,a), (2.1)
這個a 又是移位寄存器的輸入。在a的驅動下,移位寄存器的各個數據向前推進一位,使狀態變為s=(a,…..a),同時,整個移位寄存器的輸出為a。由此得到的一系列數據:a,a,a,…,a,…。該序列稱為滿足關係式(2.1)的一個反饋移位寄存器序列。
例如,線性反饋移位寄存器設f(a,a,a,…a)=ca⊕ca⊕….⊕ca⊕ca,
輸出序列{a}滿足a= ca⊕ca⊕….⊕ca⊕ca,其中i為非負整數。則該序列{a}稱為該反饋移位寄存器序列。
m序列
對於一個n級反饋移位寄存器來說,最多可以有2 個狀態,對於一個線性反饋移位寄存器來說,全“0”狀態不會轉入其他狀態,所以線性移位寄存器的序列的最長周期為2 -1。當n級線性移位寄存器產生的序列{a}的周期為T=2 -1時,稱{a}為n級m序列。
已經證明,n級m序列{ai}具有以下性質:
在一個周期內,0,1出現次數分別為2 -1次和2 次;
在一個周期圈內,總遊程(是指一個元素連續出現的次數)數為2 ,對1≤i≤n-2,長度為i的遊程有2 -1個,且0,1遊程各半,長為n-1的0遊程1個長為n的1遊程1個;
所以可以看出,該序列滿足Golomb的三個公設,具有良好的隨機特性。
當反饋函數f(a,a,a,…a)為非線性函數時,便構成非線性移位寄存器,其輸出序列為非線性序列。輸出序列的周期最大可達2 ,並稱周期達到最大值的非線性移位寄存器序列為m序列。在m序列的一個周期內,0和1的個數是相同的。在一個周期圈內,總遊程數為2 ,對1≤i≤n-2,長度為i的遊程有2 個,且0,1遊程各半,長為n-1的遊程不存在,長度為n的0遊程和1遊程各一個。
特徵多項式
對於線性反饋移位寄存器的輸出序列{a}滿足遞推關係a= ca⊕ca⊕….⊕ca⊕ca,對於任意i≥1成立。其中c=1,成為該線性移位寄存器或者該遞推關係的特徵多項式,當c≠0時,線性移位寄存器是非奇異的,有時也稱非奇異的線性移位寄存器是非退化的。