阻抗圓圖
阻抗圓圖
史密斯圖(阻抗圓圖)是一種在甚高頻和超高頻電路設計時有效地選擇計算匹配阻抗的工具。通過簡潔的作圖,代替了複雜的複數計算,使得復阻抗的匹配計算簡單明了,易學易會,是高頻領域工程師的有效工具。在國外的無線電設計領域,史密斯圖已獲得了廣泛的應用。按照複變函數的觀點,圓圖把慡複平面上的一組等值線變換到Γ複平面上,或反之。+π;或者在一張史密斯圓圖上同時套印掑、慜 和埥、埛的等值曲線簇,稱為導抗圓圖。
目錄
求解均勻無耗傳輸線有關阻抗匹配問題的一類曲線坐標圖。圖上有兩組坐標線,其中一組包括阻抗或導納的實部和虛部的等值線簇,另一組包括反射係數模值和輻角的等值線簇。所有這些等值線都是圓弧(直線是圓的特例),故稱為阻抗圓圖或導納圓圖,簡稱圓圖。
根據傳輸線理論,線上各點的歸一化輸入(視在)阻抗慡=
/
與反射係數Γ之間有如下確定關係 (見傳輸線)
(1)
式中慡 為該點的輸入(視在)阻抗;
為傳輸線的特性阻抗;
圓圖就是根據式(1)把慡和Γ 的兩組等值線套印在一張圖紙上,便於直接讀出相互換算的結果。
按照複變函數的觀點,圓圖把慡複平面上的一組等值線變換到Γ複平面上,或反之。由於式(1)表示雙線性變換的解析函數,故這種變換具有保圓性。根據變換是從慡 →Γ 還是從 Γ →慡,以及採用的是直角坐標還是極坐標,可以得到多種不同的圓圖,如史密斯圓圖、施米特圓圖和卡特圓圖等。
通過雙線性變換式(1),將慡複平面上
=常數和慜=常數的二簇相互正交的直線分別變換成複平面上的二簇相互正交的圓,其曲線方程
(2)
它們同該複平面上Γ的極坐標等值線簇常數和
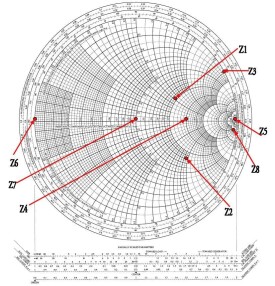
=常數組成史密斯阻抗圓圖(圖1)。
阻抗圓圖
值標度在的外圓上,而模|Γ|值從圓心至外圓作均勻標度。對於無耗線,
|,
。這裡,|Γ|和
分別為負載端反射係數的模和輻角,
為相移常數,
為工作波長,l為觀察點與負載端(參考點)的距離。習慣上在標度
時,取
=0(即
的零參考點位於
>1的實軸上),並在的外圓上標出向電源和向負載移動的波長數。例如,觀察點向電源移動
,
順時針移過180°。實際上,史密斯圓圖已被製成專用工具,附有可繞中心旋轉、標有|Γ|刻度及相應電壓駐波比
等刻度的透明標尺,使用甚為方便。
如果將阻抗慡改為導納
,同時將Γ 改為
,則有
(3)
慟 與Γ′的關係亦如式(1)中慡與Γ 的關係,因此,阻抗圓圖也可作導納圓圖使用,只須將原圖中的掑 改為埥、慜 改為 埛、
改為
′=
+π;或者在一張史密斯圓圖上同時套印掑、慜 和埥、埛的等值曲線簇,稱為導抗圓圖。慡 和慟=1/慡 的兩點在導抗圓圖上對中心點(|Γ|=0)對稱。
由於史密斯圓圖將一切阻抗值限制在單位圓內,且易於讀出反射係數值,應用最為廣泛。
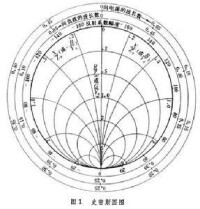
施米特圓圖
通過雙線性變換式(1),將Γ 複平面上常數和
=常數的二簇相互正交的等值線變換成慡複平面上二簇相互正交的圓,其曲線方程分別為
(4)
它們同該複平面上原有的等值線簇掑=常數和 慜=常數組成施米特阻抗圓圖,即直角阻抗坐標圖(圖2)。
阻抗圓圖
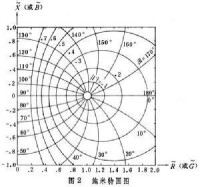
卡特圓圖
通過雙線性變換式 (1),將 慡複平面上│慡│=常數和
=常數的二簇相互正交的等值線簇分別變換成Γ 複平面上的二簇相互正交的圓,其曲線方程為
(5)
它們同該平面上原有的等值線簇常數和
=常數組成卡特阻抗圓圖 (圖3)。卡特阻抗圓圖亦可作導納圓圖使用,只需將|慡|改為|慟|、
改為-
即可。
阻抗圓圖