應力集中
物體中應力局部增高的現象
應力集中,彈性力學中的一類問題,指物體中應力局部增高的現象,一般出現在物體形狀急劇變化的地方,如缺口、孔洞、溝槽以及有剛性約束處。應力集中能使物體產生疲勞裂紋,也能使脆性材料製成的零件發生靜載斷裂。在應力集中處,應力的最大值(峰值應力)與物體的幾何形狀和載入方式等因素有關。局部增高的應力隨與峰值應力點的間距的增加而迅速衰減。由於峰值應力往往超過屈服極限(見材料的力學性能)而造成應力的重新分配,所以,實際的峰值應力常低於按彈性力學計算得到的理論峰值應力。
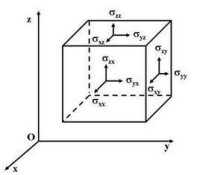
應力
應力集中是應力在固體局部區域內顯著增高的現象。多出現於尖角、孔洞、缺口、溝槽以及有剛性約束處及其鄰域。應力集中會引起脆性材料斷裂;使脆性和塑性材料產生疲勞裂紋。在應力集中區域,應力的最大值(峰值應力)與物體的幾何形狀和載入方式等因素有關。局部增高的應力值隨與峰值應力點的間距的增加而迅速衰減。由於峰值應力往往超過屈服極限(見材料力學性能)而造成應力的重新分配,所以,實際的峰值應力常低於按彈性力學計算出的理論峰值應力。
反映局部應力增高程度的參數有理論應力集中係數α,它是峰值應力和不考慮應力集中時的應力(即名義應力)的比值,它恆大於1,且與載荷的大小無關。對受單向均勻拉伸的無限大平板中的圓孔,α=3。由光滑試樣得出的疲勞極限和同樣材枓製成的缺口試樣的疲勞極限之比,稱為有效應力集中係數,它總小於理論應力集中係數,一般可由後者按經驗公式得到它的近似值。
1898年德國的G.基爾施首先得出圓孔附近應力集中的結果。1909年俄國的G.V.科洛索夫求出橢圓孔附近應力集中的公式。20世紀20年代末,蘇聯的N.I.穆斯赫利什維利等人把複變函數引入彈性力學,用保角變換把一個不規則分段光滑的曲線變換到單位圓上,導出複變函數的應力表達式及其邊界條件,進而獲得一批應力集中的精確解。各種實驗手段的發展也很快,如電測法、光彈性法、散斑干涉法、雲紋法等實驗手段(見實驗應力分析)均可測出物體的應力集中。隨著科技的進步,計算機和有限元法以及邊界元法的迅速發展,為尋找應力集中的數值解開闢了新途徑。
為了避免材料或構件因應力集中而造成的破壞,工程上主要採取以下一些措施:①表面強化:對材料表面作噴丸、滾壓、氮化等處理,可以提高材料表面的疲勞強度;②避免尖角:即把稜角改為過度圓角,適當增大過渡圓弧的半徑,效果更好;③改善零件外形;曲率半徑逐步變化的外形有利於降低應力集中係數,比較理想的辦法是,採用流線型型線或雙曲率型線,後者更便於在工程上應用;④孔邊局部加強:在孔邊採用加強環或作局部加厚均可使應力集中係數下降,下降程度與孔的形狀和大小、加強環的形狀和大小以及載荷形式有關;⑥適當選擇開孔位置和方向:開孔的位置應盡量避開高應力區,並應避免因孔間相互影響而造成應力集中係數增高,對於橢圓孔,應使其長軸平行於外力的方向,這樣可降低峰值應力;⑥提高低應力區應力,減小零件在低應力區的厚度,或在低應力區增開缺口或圓孔,使應力由低應力區向高應力區的過渡趨於平緩;⑦利用殘餘應力:在峰值應力超過屈服極限后卸載,就會產生殘餘應力,合理地利用殘餘應力也可降低應力集中係數。
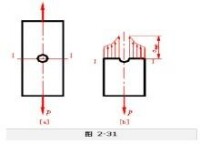
帶圓孔的板條
