反算
反算
反算(Inversion )是指根據直線的起點和終點的坐標,計算直線的水平距離和坐標方位角的過程。
坐標反算是指根據直線的起點和終點的坐標,計算直線的水平距離和坐標方位角的過程。坐標反算一般主要應用於測繪工程、建設工程之中,具體在建築設計,工程測量,測繪製圖等領域。總的來說坐標計算分為坐標正算和坐標反算兩種,這兩種在實際中是較常見的。
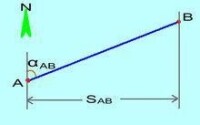
如圖中所示,已知一條直線的起點和終點坐標分別為A點坐標(),B點坐標,A點到B點距離L,A點到B點方位角,通過坐標反算來計算直線AB的水平距離和坐標方位角。
坐標正算公式:
坐標反算公式:
由於反三角函數計算的結果有多值性
反算
①;
②;
③。L是A、B兩點間距離,是水平距離。
④根據“②”中所求的,求坐標方位角,
⑴若坐標方位角為第一象限角,則:;
⑵若坐標方位角為第二象限角,則:;
⑶若坐標方位角為第三象限角,則:;
⑷若坐標方位角為第四象限角,則: 。
坐標方位角:直線的方向是用方位角來表示的,其中以坐標北方向為基準方向,順時針旋轉到直線的水平角度,稱為該直線的坐標方位角。
象限角劃分:第一象限角:
第二象限角:
第三象限角:
第四象限角:
另注意:此象限角的劃分與數學中的象限角不同,應注意!
反算
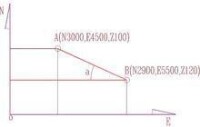
從E坐標可以發現,B點E坐標大於A點,所以B點應在A點的東面。再看B的N坐標小於A點,故B點應在A點南面。即B點在A點東南面。
求出直線AB與E坐標的夾角:
若,則直線從A到B成右上方向走向。若,則直線從A向B成左下方向走向。若,則AB平行於E軸線。若,則直線垂直於E軸線。由此可以確定現場的NE坐標系。
縱觀目前國內外的反算方法,主要可分為五類,即:圖表法和回歸公式法、迭代法、資料庫搜索法遺傳演演算法和人工神經網路法國外各類反算方法的主要軟體如表1所示。
根據常見的路面結構,在較大範圍內選取不同模量Ej和厚度hj的結構組合,通過彈性層狀體系理論計算各結構組合的理論彎沉盆W,並運用多元回歸分析方法,建立 的統計關係式,或者編繪成計算圖表由此,將實測彎沉盆數據和厚度參數代入統計公式或圖表,從而確定路面各結構層的模量這類方法具有快速和方便的優點,適合於野外現場評定其主要缺點包括:
(1)由於彈性層狀體系理論的複雜性,W與Ej之間並不存在簡單的統計相關關係,因此,這類方法的反算精度差;
(2)通用性差,當模量、厚度結構層數等參數超出回歸公式或計算圖表的計算範圍時,將無法處理。
首先假設一組結構層模量(初始值),採用力學分析方法計算理論彎沉盆,並與FWD實測彎沉盆進行比較,根據彎沉差異確定模量修正值,從而獲得一組新的模量然後,以此作為下輪迭代的初始值,不斷重複這一迭代過程,直至滿足預先給定的收斂精度或迭代次數的要求為止實際上,模式識別法也是根據這種迭代原理進行反算魄這類方法將模量反算視為非線性規劃問題,從而採用數學規劃法中的不求導數的直接搜索或者近似求導的梯度搜索等啟髮式最優化演演算法進行計算其優點是,在一般情況下,反算結果精度高,便於引入各種不同的力學分析模型,具有良好的可擴展性主要缺點包括:
(1)由於這類方法需要大量的迭代計算。其計算速度相對較慢;
(2)根據最優化方法的理論,對於非線性優化問題,數學規劃法無法避免初始值和局部收斂的問題,使得模量反算存在受初始值迭代方法和收斂標準影響大和局部極小的缺點;
(3)在許多演演算法中,為了保證收斂,需要給定較嚴格的模量取值範圍,雖然在一定程度上降低了結果發散的可能性,但並不能從根本上解決初始值和局部收斂的問題,同時,限制模量的取值也影響了演演算法的適用範圍;
( 4)路面結構的土基模量隨彎沉的變化較敏感,而結構層模量隨彎沉變化不敏感,因此,當選取的收斂標準和迭代次數不合適時,往往反算的土基模量結果穩定,而結構層的模量誤差大
預先對需要分析的路面結構,選取大量的模量論彎沉盆,並將理論計算結果以資料庫的形式保存,形成理論彎沉盆的資料庫。然後,採用直接搜索法和插值技術,尋找滿足彎沉盆擬合精度要求的模量組念其中以MODULUS反算程序最為著名,這種方法的主要優點是計算速度快,收斂穩定,適合於路網普查,這也是美國SHRP計劃通過比較、篩選決定選用MODULUS的主要原因這種方法的主要缺點包括:
(1)理論彎沉盆資料庫需要耗費大量的存儲空間,並且,對於資料庫中沒有的路面結構形式,需要重新計算,形成新的彎沉盆資料庫,耗時較長;
( 2)雖然反算總能收斂,但由於採用了插值方法,反算結果可能誤差很大,其反算方法採用最優化方法中的直接搜索法,無法從根本上避免初始值和局部極小問題;
(3)需要選取較為嚴格的模量取值範圍,演演算法通用性較差。
預先在給定的模量範圍內,隨機產生一定數量的模量組合,將各組合轉換成不同的數字串(染色體),形成原始種群。通過力學分析計算各組合的理論彎沉盆,以理論彎沉盆和FW D實測彎沉盆之間的誤差作為適度函數,對各染色體的適度進行評仇然後,按照一定的概率對種群的染色體進行選擇、交叉和變異等遺傳計算,形成新的種群。以新的種群作為原始種群,重複上述迭代過程,直至滿足給定的收斂標準或迭代次數為止,並從最後一代種群中選取彎沉擬合精度最好的染色體作為反算的模量結果遺傳演演算法是一種模擬自然選擇法則的最優化演演算法,其實質是一種迭代自適應啟髮式概率性搜索演演算法,可解決不同的非線性問題的魯棒性和全局最優性。
因此,具有精度高和全局收斂的優點,並很好地解決了初始值的問題其主要缺點包括:
(1)由於遺傳演演算法是對自然選擇過程的模擬,只有經過大量的遺傳計算,才能獲得穩定的結果,因此,其計算速度很慢,無法滿足工程應用中大規模反算的要求;
(2)種群染色體個數的選取缺乏理論指導,規模太小容易導致早熟,無法獲得穩定的結果,規模太大則大幅降低計算速度;
(3)需要合理地預測模量的取值範圍,確定合適的染色體長度,超出取值範圍的誤差將很大
利用人工神經網路的高度非線性映射能力,預先通過力學理論計算,獲得大量的模量厚度和荷載等參數組合的理論彎沉盆結果,作為神經網路的訓練樣本。然後,選取合適的網路模型和學習演演算法,以彎沉厚度與荷載等參數作為輸入,模量作為輸出,訓練神經網路。經過反覆訓練,訓練好的神經網路即可作為路面模量反算的工具。由於採用訓練好的神經網路進行模量反算時,只需數次簡單的整合與傳遞函數的運算,因此,神經網路法是目前反算速度最快的方法,具有實時處理的優點。其主要缺點包括:
(1)由於神經網路是一種近似計算方法,反算結果的精度取決於網路結構和規模訓練樣本的容量和代表性及學習演演算法的收斂性等因素,因此,一般誤差較大;
(2)由於FW D存在各種系統和人為誤差,以及路面結構力學分析模型的簡化,實測彎沉盆不可能無限逼近理論彎沉盆,二者之間必然存在誤差,為了消除該種誤差對反算結果的影響。必須在訓練樣木中加入噪音數據,以獲得神經網路的魯棒性,否則,採用訓練好的網路進行反算時,對理論彎沉盆可以獲得高精度的結果,而對實測彎沉盆,必然會得到不合理的結果,因此,對於人工神經網路法,噪音處理至關重要,然而,對於噪音數據的選取,主要依靠經驗,缺乏理論指導;
(3)目前普遍採用BP網路進行反算,而BP網路的學習演演算法存在初始值和局部極小問題,同時,其隱單元數的確定也缺乏理論指導
從五類反算方法的優缺點可看出,未來仍需對模量反算方法開展深入研究,在滿足大規模反算要求的基礎上,重點解決以下三個關鍵問題。
非線性最優化方法一般都需要從初始值開始迭代,初始值不管是給定的還是隨機產生的,演演算法本身的局部收斂性決定了反算結果的局部收斂性。同時,由於彎沉誤差等值線具有狹長和平坦分佈的特點,收斂標準的允許誤差對反算結果的精度有很大的影響,過於苛刻勢必造成迭代振蕩而降低計算速度,過於寬鬆迭代會提前終止而影響結果的精度。因此,尋找從數學上嚴格證明的受初始值影響小且具有大範圍收斂的方法是未來研究方向之一,同倫方法為此提供了新途徑。
一般情況下,不同的收斂標準獲得的反算結果是不相同魄由於模量反算屬於非線性最優化問題,在某一收斂標準下可能會存在多個解的情況(一般較少出現)因此,為了解決唯一性的問題,一方面需要通過試驗驗證,選取合理的收斂標準;另一方面可通過選取合理的位移感測器布置方案,減少或避免多解的情況同時,從非線性最優化理論方面開展多解的研究,以合理取捨反算結果
由於反算結果屬於二級指標,所以應加強反算結果與試驗結果的驗證研究,比較分析反算結果的合理性,並用於路面評價和設計,同時,目前模量反算的正分析大多採用彈性層狀體系理論,由於路面結構層材料的非線性性質和FWD動載的特點,需進一步開展非線性和動載等動參數的反算研究
另外,模量反算時,路面結構層厚度一般按設計值選取,或者根據有限的鑽孔檢測結果確定實際上。由於施工變異性的影響,以及行車荷載和自然環境等因素的作用,實際厚度與反算取值之間存在著差異,而這種差異對反算結果有著較大的影響。因此,為了減小厚度取值的誤差,未來應加強在FWD檢測的同時,配合採用路面雷達等無損檢測技術測定路面結構層的厚度。