共找到3條詞條名為平移的結果 展開
- 向同一方向移動相同距離的運動
- 機械運動的特殊形式之一
- 平移變換
平移
向同一方向移動相同距離的運動
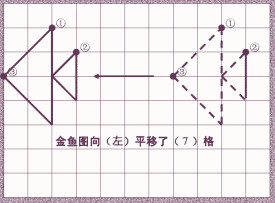
平移,是指在同一平面內,將一個圖形上的所有點都按照某個直線方向做相同距離的移動,這樣的圖形運動叫做圖形的平移運動,簡稱平移。
平移不改變圖形的形狀和大小。圖形經過平移,對應線段相等,對應角相等,對應點所連的線段相等。它是等距同構,是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上,或將坐標系統的中心移動所得的結果。即是說,若是一個已知的向量,是空間中一點,平移。
圖片平移的方向,不限於是水平。
在仿射幾何,平移(translation)是將物件的每點向同一方向移動相同距離。
它是等距同構,是仿射空間中仿射變換的一種。它可以視為將同一個向量加到每點上,或將坐標系統的中心移動所得的結果。即是說,若v是一個已知的向量,p是空間中的一點,平移。
將同一點平移兩次,結果可用一次平移表示,即,因此所有平移的集是一個群,稱為平移群。這個群和空間同構,又是歐幾里德群E(n)的正規子群。
T對E的商群與正交群同構:。
經過平移,對應線段平行(或共線)且相等,對應角相等,對應點所連接的線段平行且相等。
平移變換不改變圖形的形狀、大小和方向(平移前後的兩個圖形是全等形)。
(1)圖形平移前後的形狀和大小沒有變化,只是位置發生變化。
(2)圖形平移后,對應點連成的線段平行(或在同一直線上)且相等。
(3)多次連續平移相當於一次平移。
(4)偶數次對稱后的圖形等於平移后的圖形。
(5)平移是由方向和距離決定的。
(6)經過平移,對應線段平行(或共線)且相等,對應角相等,對應點所連接的線段平行(或共線)且相等。
這種將圖形上的所有點都按照某個方向作相同距離的位置移動,叫做圖形的平移運動,簡稱為平移
平移的條件:確定一個平移運動的條件是平移的方向和距離。
1原來的圖形的形狀和大小和平移后的圖形是全等的。
2平移的方向。(東南西北,上下左右,東偏南n度,東偏北n度,西偏南n度,西偏北n度)
3平移的距離。(長度,如7厘米,8毫米等)
1.通過簡單的平移可以構造精美的圖形。也就是花邊,通常用於裝飾,過程就是複製-平移-粘貼。
2.平移常與平行線有關,平移可以將一個角,一條線段,一個圖形平移到另一個位置,是分散的條件集中到一個圖形上,使問題得到解決。
1把一個圖形整體沿某一直線方向移動,會得到一個新的圖形,新圖形與原圖形的形狀和大小完全相同。
2新圖形中的每一點,都是由原圖形中的某一點移動后得到的,這兩個點是對應點。連接各組對應點的線段平行且相等(或在同一直線上)。
1平移前後圖形的形狀、大小不變,只是位置發生改變。
2新圖形與原圖形的對應點所連的線段平行且相等(或在同一直線上)。
3新圖形與原圖形的對應線段平行且相等,對應角相等。
以畫雪人為例。可以把半透明紙蓋在圖上,先描出一個雪人,然後按同一方向陸續移動這張紙,再描出第二個、第三個……而求必須水平或垂直於原圖。根據平移的方向,作出每一個圖形要點的平移點(如:直線的頂點,圓的圓心等)
方法是通過原來圖形的點作平移方向的平行線,並取距離為平移的長度的點 用三角板的話,第一塊三角板斜邊對齊平移方向;第二塊三角板斜邊貼住第一塊三角板的直角邊作為第一塊三角板移動的準線(之後第二塊三角板必須保持固定);第一塊三角板沿著第二塊三角板斜邊移動到相應的點,輕輕畫出平行線(以後要擦除),在平行線上量出平移的距離的點就是目標“平移點”;2,根據平移點,作出原來的圖形(如:直線只要直接連接兩個端點,以平移圓心為圓心作等半徑的圓。
(1)找出原圖形的關鍵點(如頂點或者端點);
(2)按要求分別描出各個關鍵點平移后的對應點;
(3)按原圖將各對應點順次連接。
例如在三維空間,使用齊次坐標,可用矩陣表示為