三角形中位線

證明1：

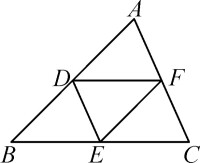
如圖，延 長DE 到 F，使EF=DE ，連 結CF。

∵DE=EF ∠AED=∠CEF AE=EC

∴△ADE ≌ △CFE（SAS）

∴AD=FC ∠A=∠ECF

∴AB∥FC

又∵AD=DB

∴BD∥CF，BD=CF

∴四邊形BCFD是平行四邊形

∴DE∥BC 且 DE=1/2BC

證明2：

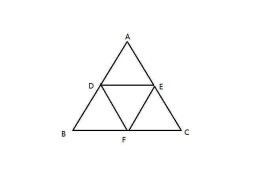
如圖，延 長DE 到 F，使EF=DE ，連 結CF、DC、AF

∵AE=CE DE=EF

∴四邊形ADCF為平行四邊形

∴AD∥CF，AD=CF

∵AD=BD

∴BD∥CF，BD=CF

∴四邊形BCFD為平行四邊形

∴BC∥DF，BC=DF

∴DE∥BC 且 DE=1/2BC

誤區：要把三角形的中位線與三角形的中線區分開。三角形中線是連結一頂點和它對邊的中點，而三角形中位線是連結三角形兩邊中點的並且與底邊平行且等於底邊一半的的線段。

初等平面幾何中，有關三角形中位線的定理：“三角形的中位線平行於底邊，且等於底邊的一半。”及“過三角線一 邊的中點且平行於另一邊的直線必過第三邊的中點。”在幾何題的證明中應用十分廣泛。

其原因是由於定理中有平行線出現，這樣就產生了同位角、內錯角、同旁內角等許多角之間的等量關係，又由於中位線等干底邊的一半。並且平分兩腰，這樣就出現了線段之間的等量關係。更主要的是定理將角的等量關係與線段的等量關係有機地聯繫在 一起，因此這個定理在幾何題的證明中，特別是在證明兩直線平行或線段的等量關係或角的等量關係中，起著獨特的作用，有時甚至非它莫許。因此凡是題設中有中點出現，就不妨設法應用中位 線定理來進行證明，也許很有效。下面舉幾個實例來加以說明。

例：AD是△ABC的外接圓⊙o的直徑(D點不與BC點重合)，過D作⊙o 的切線交BC於P，連線OP交AB、AC 於 M、N，求證OM=ON。

分析：從題目所給的條件與所要證明的結論來看，沒有明顯的聯繫，為此需要添加輔助線，勾通條件與結論的聯繫。

鑒於M、N分別在AB、AC邊上的一般位置。若過B點作BE//MN分別交AC、AD於E、F，則證明OM= ON就可 轉化為證明BF=EF，也即是要證明F為BE的中點，這時B點在⊙o 上，和題設條件有了明顯的聯繫。在△BCE中BC 是⊙o 的弦。取BC的中點G，如果能證明FG是△BCE的中位線，問題就解決了、因此只須要證明 FG//CE 就行了。而要證明這一 點是非常容易的事情。

證明：因OD⊥PD、 OG⊥BC、

故O、P、D、G 四點共圓

從而∠FDG=∠OPG

又因BE//OP，故∠OPC=∠FBG

所以∠FDG =∠FBG

因此B、D、G、F四點共圓

所以∠FGB =∠FDB( 或∠FGB一兀一∠FDB )

又因為∠FDB =∠ACB( 或∠ACB 一∠兀一FDB )

所 以∠FGB =∠ACB，從而FG//CE

而G為BC的中點，由中位線定理，可知

F是BE的中點，即BF=EF

由於FB分之OM=AF分之AO=FE分之ON

所以OM=ON

現代教育的功能，必須由訓練記憶、選拔以及向訓練素質、促進發展方向轉變。教育教學方法和手段必須更加先進，通過優化學生的學習過程，優化教學方法，促進素質教育的實施。著名教育家布魯納認為：“知識的獲得是一個主動的過程，學習者不應該是信息的被動接受者，而應該是知識獲取的主動參與者。”由此可見，在課堂教學活動中，教師應充分發揮主導作用，從愛護和培養學生的好奇心、求知慾出發，幫助學生自主學習獨立思考，保護學生的探索精神，創新思維，營造崇尚真知，追求真理的氛圍，為學生的稟賦和潛能的充分開發創造一種寬鬆的環境。為此，課堂教學一定要分層遞進，當代教育家顧冷沅先生認為：“把握好推動學習前進的適度序列，是課堂教學的生命線”在新知識的教學活動中，教師要利用學生已有的知識點，這些知識點與新知識的聯繫有一定的或近或遠的距離，這個距離就是學習前進的梯度。教師在刻苦鑽研教材的基礎上，要對課堂教學進行多方面，多角度研究、提煉、摘選分層遞進的最佳方案，用電教媒體顯示新知識的產生和形成過程，給學生觀察、思考和探索的時間，讓學生成為學習過程中的發現者、參與者，培養學生的創新精神。例如三角形中位線的課堂教學可分四個步驟進行：

定理的產生過程

用投影顯示： ΔABC 中， AD =BD， AE=CE，DE 與BC有什麼關係 ?

問同學們能用語言來敘述這一結論嗎?

由於教科書受到各種因素的限制，大部分知識都是直接給出，省去了其產生和形成過程。如果教師都直接按課本把知識拋給學生，“直接了當”固然節約了時間，但對於學生來說，缺乏一個完整的認知過程。把知識或方法不是作為過程，而是作為結果直接拋給學生，長此以往越拋越多，學生在頭腦中很難形成一個良好的認知結構。因此，課堂教學要呈現知識的發生過程，才能激發學生探索問題、思考問題的積極性，通過學生自己發現概括出結論，不僅培養學生的創新精神，而且提高了學生的觀察能力、抽象能力和概括能力，同時也使學生對新學的定理有深刻的印象。

定理的證明過程

1、要證明一個命題的正確性，首先要做什麼?(引導學生分清題設，結論，畫好圖形，寫出已知、求證)；

2、一般在什麼圖形中的線段相等和平行?

(引導學生用平行四邊形、三角形全等等來證三角形中位線定理，進而按照他們的思維進行探討：)

怎樣作輔助線才能把DE、BC放在平行四邊形和三角形中？發現：延長中位線DE到F，使EF=DE，連結CF，由ΔADE≌CFE得AD//且=CF；根據對角線互相平分，判定四邊形ADCF是平行四邊形得AD//且=CF；過C作CF//AB，與DE的延長線交於點 F，也可以證明AD//且=CF，再由BD=AD，得BD//且=CF，所以四邊形DBCF是平行四邊形，DF//且=BCF，因為 DE=2分之1 DF，所以DE//且=2分之1BC。

3、要證明三角形中位線定理還可用什麼方法?

(引導學生從新的角度去思考，探索解決問題的新途徑，引導學生用上節課學的平行線等分線定理 來證)；

4、引導學生寫出證明過程(強調每個學生獨立去完成)；

5、引導學生總結解決問題的經驗(讓學生充分發表自己的見解)：

從學生最熟悉的知識點出發，通過階梯進性的點撥，著重培養和提高學生分析問題、解決問題的能力；由一題多證，著重培養學生的發展思維能力。

定理的應用

例1、在ΔABC中，已知 AB=8cm，BC=10cm，CA=12cm，D、E、F分別是AB、BC、AC邊上的中點，求ΔDEF的周長。

分析提問：

(1)D、E、F 分別是AB、BC、AC邊上的中點，則DE、EF、DF是ΔABC的什麼線 ?

(2)AB=8cm，則EF=? BC=10cm，則DF=?AC=12cm，則DE=?

(3)ΔDEF的周長是什麼 ? 能否自己寫出解的過程 ? 直接運用定理，固鞏新知。

例 2、求證：順次連結四條邊的中點，所得的四邊形是平行四邊形。

分析提問：

(1)這是一道文字命題，要解決這一問題首先要做什麼?

(引導學生根據命題畫圖，寫出知已、求證)

(2)一般情況下，要證明一個四邊形是平行四邊形有哪些方法? (引導學生思考證明一個四邊形是平行四邊形的常用方法：兩組對邊分別平行，兩組對邊分別相等，一組對邊平行相等，等等)。

(3)命題中有“ …四邊中點 ……”引導學生從新的角度思考，探索解決問題的新途徑，從直覺思維出發，此題與三角形的中位線定理有關，構建三角形，作輔助線連結BD，利用三角解形中位線定理證。

在這裡著重培養學生提取信息“ ……中點 … …”是與三角形中位線有關的，由此信息進行聯想，產生對信息的加工，處理，轉換成要證EH//且=FG，只要證EH//且=2分之1BD，FG//且=2分之1BD即可。達到培養學生解決問題的創新性，提高學生的創造思維能力。

鞏固提高

以提高學生處理綜合問題的能力。

分層遞進的課堂教學，面向全體學生，在承認學生個性差異的前提下，因材施教，使知識的發生、發展規律與學生的認識規律有機地結合起來，同步進行曲。實施分層教學，分層練習，分層講評，分層矯正，讓各層次的學生在課堂里既各有所得達到基本要求，又能使他們的智能盡量得到發展，差生逐步向中等生轉化，中等生向優等生轉化，使全體學生的素質得到全面提高。